Imagine isto: você está comprando online um laptop de alto desempenho.
Você clica em um, e várias sugestões semelhantes aparecem. Elas são próximas do que você está procurando, mas não são exatamente iguais. Como o site sabe quais são relevantes para sua busca?
É aqui que entra a similaridade cosseno – uma ferramenta matemática que mede a similaridade entre dois vetores não nulos em um espaço de alta dimensão.
Bancos de dados vetoriais em motores de busca e sistemas de recomendação usam a similaridade cosseno para entender quão próximos produtos ou consultas de busca em um banco de dados se correspondem com base em suas representações vetoriais. Compreender esses relacionamentos e padrões entre itens permite que soluções de banco de dados vetorial recuperem sugestões personalizadas e precisas que mantêm você navegando – e talvez até comprando.
O que é similaridade cosseno?
A similaridade cosseno é uma métrica matemática que mede a similaridade entre dois vetores em um espaço de produto interno ou multidimensional. Ela usa o cosseno do ângulo entre dois vetores para determinar se eles apontam na mesma direção, independentemente de suas magnitudes.
Em outras palavras, a similaridade cosseno é o produto escalar de dois vetores dividido pelo produto de suas magnitudes. Também é conhecida como similaridade de Orchini e coeficiente de congruência de Tucker.
Cientistas de dados, engenheiros de aprendizado de máquina e desenvolvedores de software usam a similaridade cosseno para comparar milhares de pontos de dados e entender seus relacionamentos sem se perder nos detalhes. É amplamente utilizada para medir similaridade em mineração de texto, recuperação de informações e aplicações de análise de texto.
Outras medidas de similaridade populares incluem distância Euclidiana, distância de Manhattan, similaridade de Jaccard e distância de Minkowski.
Por que a similaridade cosseno é importante?
A similaridade cosseno fornece uma maneira robusta de avaliar a similaridade semântica entre documentos, conjuntos de dados e imagens de alta dimensão e esparsos. É eficaz porque foca na orientação de dois vetores em um espaço, medindo sua similaridade independentemente de sua magnitude.
Aplicações de análise de texto usando frequência de termo-inverso de frequência de documento (TF-IDF), Word2Vec e representações de codificador bidirecional de transformadores (BERT) derivam vetores de palavras com grandes dimensões, mas baixa sobreposição. Métricas de similaridade tradicionais como a distância Euclidiana são sensíveis aos comprimentos dos vetores e não conseguem lidar com esses vetores. A similaridade cosseno pode facilmente focar na correlação de dados em tais cenários.
A similaridade cosseno também ajuda aplicações de recuperação de informações a classificar documentos com base em quão bem eles correspondem a uma consulta, mesmo quando os documentos variam em comprimento ou complexidade.
A escalabilidade da similaridade cosseno em espaço vetorial de alta dimensão a torna inestimável para bancos de dados vetoriais, onde encontrar vizinhos mais próximos de forma rápida e precisa é necessário para recuperação de imagens, sistemas de recomendação e detecção de anomalias.
O processamento de linguagem natural (NLP) depende da similaridade cosseno para comparar eficientemente incorporações vetoriais. Essa comparação de incorporações auxilia algoritmos de NLP na classificação, agrupamento ou recomendação de conteúdo com base na similaridade semântica de documentos.
Quer aprender mais sobre Software de Banco de Dados Vetorial? Explore os produtos de Banco de Dados Vetorial.
Como a similaridade cosseno funciona?
A similaridade cosseno quantifica a similaridade entre dois vetores calculando o cosseno do ângulo entre eles. Abaixo está a explicação de como a similaridade cosseno funciona em ambientes de dados esparsos e de alta dimensão.
- Representação vetorial: O primeiro passo envolve converter objetos como palavras, documentos, imagens ou textos em vetores em um espaço de alta dimensão. Cada dimensão do vetor representa um único objeto, com seu valor mostrando a frequência do vetor ou sua importância.
- Produto escalar: O produto escalar quantifica o relacionamento entre dois vetores multiplicando seus componentes correspondentes e somando os resultados. Calcular esse produto escalar é vital para entender o alinhamento entre vetores na mesma direção.
- Cálculo de magnitude: O próximo passo envolve calcular os comprimentos ou magnitudes de cada vetor.
- Similaridade cosseno: A pontuação de similaridade cosseno é o produto escalar dividido pelo produto das magnitudes dos dois vetores.
Dividir o produto escalar pelo produto das magnitudes dos vetores normaliza o resultado da similaridade para um intervalo entre -1 e 1. Essa normalização garante que a pontuação de similaridade reflita apenas o ângulo de orientação dos vetores, não sua magnitude. Mede consistentemente a similaridade dos vetores, independentemente da escala dos dados.
Como calcular a similaridade cosseno
Calcular a similaridade cosseno requer encontrar o produto escalar de dois vetores. Em seguida, multiplique as magnitudes desses dois vetores. Agora, divida o produto escalar pelo produto das magnitudes para encontrar a pontuação de similaridade cosseno.
Fórmula de similaridade cosseno
A pontuação de similaridade cosseno entre dois vetores, A e B, é calculada usando a fórmula abaixo:
Similaridade Cosseno (A, B) = (A·B) / (||A|| * ||B||)
Onde,
A · B é o produto escalar dos vetores A e B
||A|| e ||B|| representam o comprimento ou magnitude dos dois vetores A e B
||A|| * ||B|| denota o produto das magnitudes dos vetores A e B
A similaridade cosseno varia entre -1 e 1.
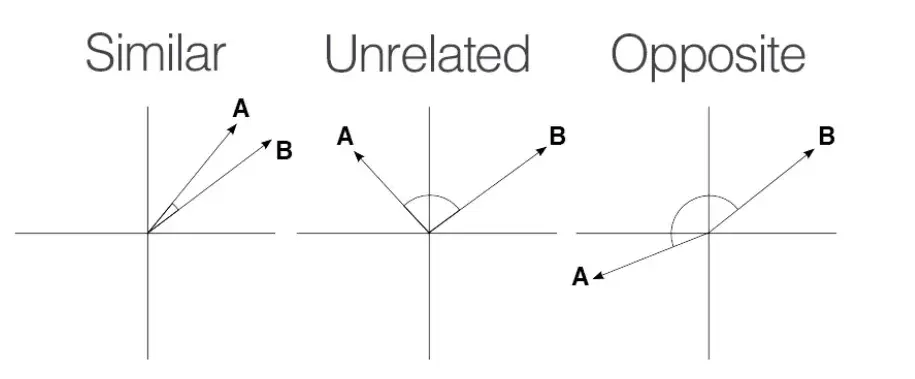Fonte: Medium
Uma pontuação de 1 significa que os vetores estão perfeitamente alinhados ou proporcionais, indicando máxima similaridade.
Uma pontuação de 0 implica que os vetores são ortogonais, significando que não têm similaridade.
Uma pontuação de -1 mostra que os vetores são perfeitamente opostos, significando que apontam em direções opostas, mas têm a mesma magnitude.
Exemplo de similaridade cosseno
Vamos calcular a similaridade cosseno entre os vetores A e B.
O vetor A tem valores, A = { 1, 9, 3, 6 } O vetor ‘B’ tem valores, B = { 1, 7, 0, 1 }
Produto Escalar: A·B = 1×1 + 9×7 + 3×0 + 6×1 =70
Magnitude de A: ||A|| = √(1² + 9² + 3² + 6²) = √(1 + 81 + 9 + 36) = √127 ≈ 11.27
Magnitude de B: ||B|| = √(1² + 7² + 0² + 1²) = √(1 + 49 + 0 + 1) = √51 ≈ 7.14
Similaridade Cosseno = (A · B) / (||A|| * ||B||) = 70 / (11.27 × 7.14) ≈ 0.87
A similaridade cosseno entre os vetores A e B é aproximadamente 0.87, o que mostra uma similaridade substancial entre eles.
Bibliotecas para cálculo de similaridade cosseno
Calcular a similaridade cosseno é simples, mas pode ser difícil ao trabalhar com grandes conjuntos de dados. Nessas situações, você pode usar linguagens de programação como Python e bibliotecas e ferramentas como Matlab, SciKit-Learn, TensorFlow e SciPy.
NumPy
NumPy é uma poderosa biblioteca Python para cálculos numéricos. Ela suporta operações de arrays multidimensionais, matrizes e funções matemáticas, tornando-a ideal para cálculos de similaridade cosseno.
Como calcular a similaridade cosseno usando NumPy
# importar bibliotecas necessárias
import numpy as np
from numpy.linalg import norm
# definir duas listas ou array
A = np.array([1, 9, 3, 6])
B = np.array([1, 7, 0, 1])
print("A:", A)
print("B:", B)
# calcular similaridade cosseno
cosine = np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B))
print("Similaridade Cosseno:", cosine)
SciKit-Learn
SciKit-Learn é uma biblioteca de aprendizado de máquina baseada em Python com funções integradas para tarefas de análise de dados, incluindo similaridade cosseno. O módulo sklearn.metrics.pairwise oferece uma função cosine_similarity para lidar com matrizes densas e esparsas.
Como calcular a similaridade cosseno usando SciKit-Learn
# importar bibliotecas necessárias
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
# definir os vetores
A = np.array([[1, 9, 3, 6]])
B = np.array([[1, 7, 0, 1]])
# calcular similaridade cosseno
cosine_sim = cosine_similarity(A, B)
print("Similaridade Cosseno:", cosine_sim[0][0])
SciPy
SciPy é outra biblioteca popular baseada em Python para computação científica. Construída sobre o NumPy, a SciPy possui funções otimizadas que calculam a similaridade cosseno para grandes conjuntos de dados. O módulo scipy.spatial.distance inclui uma função de cálculo de distância cosseno, que você pode usar para calcular a similaridade cosseno.
Como calcular a similaridade cosseno usando SciPy
# importar bibliotecas necessárias
import numpy as np
from scipy.spatial.distance import cosine
# definir os vetores
A = np.array([1, 9, 3, 6])
B = np.array([1, 7, 0, 1])
# calcular distância cosseno
cosine_distance = cosine(A, B)
# calcular similaridade cosseno
cosine_similarity = 1 - cosine_distance
print("Similaridade Cosseno:", cosine_similarity)
Gensim
Gensim é uma biblioteca Python amplamente utilizada para modelagem de tópicos e processamento de linguagem natural. Ela possui funções integradas para calcular a similaridade cosseno entre um grande volume de documentos de texto e vetores de palavras.
Como calcular a similaridade cosseno usando Gensim
# importar bibliotecas necessárias
from gensim import corpora
from gensim.matutils import sparse2full
from gensim.similarities import MatrixSimilarity
from gensim.models import TfidfModel
import numpy as np
# documentos de exemplo
documents = [
"Eu amo jogar futebol.",
"Futebol é um ótimo esporte.",
"Eu gosto de assistir filmes.",
"Filmes são divertidos.",
]
# tokenizar e pré-processar
texts = [[word.lower() for word in doc.split()] for doc in documents]
# criar um dicionário e corpus
dictionary = corpora.Dictionary(texts)
corpus = [dictionary.doc2bow(text) for text in texts]
# criar um modelo TF-IDF
tfidf_model = TfidfModel(corpus)
tfidf_corpus = tfidf_model[corpus]
# criar um índice de similaridade
index = MatrixSimilarity(tfidf_corpus)
# calcular a similaridade do primeiro documento com todos os outros
similarities = index[tfidf_corpus[0]]
# imprimir as similaridades
print("Similaridades Cosseno para o Documento 0:", similarities)
TensorFlow e PyTorch
TensorFlow e PyTorch são bibliotecas populares de aprendizado profundo que ajudam a medir a similaridade entre vetores de características de alta dimensão.
Como calcular a similaridade cosseno usando TensorFlow
# importar bibliotecas necessárias
import tensorflow as tf
# definir os vetores
A = tf.constant([1.0, 9.0, 3.0, 6.0])
B = tf.constant([1.0, 7.0, 0.0, 1.0])
# calcular similaridade cosseno
def cosine_similarity(A, B):
# calcular o produto escalar
dot_product = tf.reduce_sum(A * B)
# calcular a norma (magnitude) dos vetores
norm_A = tf.sqrt(tf.reduce_sum(tf.square(A)))
norm_B = tf.sqrt(tf.reduce_sum(tf.square(B)))
# calcular similaridade cosseno
cosine_sim = dot_product / (norm_A * norm_B)
return cosine_sim
similarity = cosine_similarity(A, B)
print("Similaridade Cosseno:", similarity.numpy())
# calcular similaridade cosseno
cosine_similarity = 1 - cosine_distance
print("Similaridade Cosseno:", cosine_similarity)
Ao usar PyTorch, os desenvolvedores podem usar torch.tensor() para criar objetos tensor e usar a função torch.norm() para calcular a norma Euclidiana dos vetores.
Considere usar as dicas abaixo para otimizar cálculos de cosseno em Python:
- Opte por bibliotecas otimizadas. Use operações vetorizadas do NumPy ou SciKit-Learn para calcular a similaridade cosseno e reduzir a sobrecarga de loops em Python. Essas bibliotecas também têm desempenho mais rápido do que o Python básico.
- Use Numba. Numba é um compilador just-in-time (JIT) de código aberto para código Python e NumPy. Ele ajuda a paralelizar automaticamente cálculos de similaridade cosseno usando múltiplas unidades de processamento central (CPUs).
- Empregue matrizes esparsas. Considere usar representações de matrizes esparsas do SciPy ao lidar com conjuntos de dados com múltiplos valores zero. Isso ajudará a economizar memória e tempo de computação para tarefas de análise de similaridade de texto e documentos.
- Use Cython para compilação de código. Cython permite que desenvolvedores escrevam códigos semelhantes a C com uma sintaxe semelhante a Python. Usá-lo para compilação de código ajuda a alcançar velocidades semelhantes a C ou C++ enquanto mantém a facilidade da sintaxe Python.
- Use algoritmos ANN. Algoritmos de vizinhos mais próximos aproximados ou ANN, como KD-Trees ou hashing sensível à localidade (LSH), ajudam a encontrar vetores semelhantes sem calcular a similaridade cosseno. Esses algoritmos podem ser benéficos para aplicações em larga escala.
- Acesse GPUs. Usar unidades de processamento gráfico ou GPUs com bibliotecas Python como TensorFlow também pode ajudar a alcançar maior rendimento ao trabalhar com extensos conjuntos de dados de alta dimensão.
Similaridade cosseno vs. outros métodos para cálculo de similaridade
A similaridade cosseno não é o único método para medir a similaridade entre objetos em um conjunto de dados. Outros métodos populares de cálculo de similaridade são:
Distância Euclidiana
A distância Euclidiana mede a distância em linha reta entre dois pontos no espaço Euclidiano. Ela é sempre zero ou positiva. Você pode não conseguir encontrar uma distância Euclidiana significativa em espaços de alta dimensão, pois os pontos tendem a convergir.
A similaridade cosseno é ideal para dados de alta dimensão ou análise de texto onde a magnitude do vetor não é essencial. A similaridade Euclidiana funciona melhor para espaços de baixa dimensão onde a magnitude do vetor é vital.
Distância de Manhattan
Esta mede a distância entre dois pontos em um caminho semelhante a uma grade somando as diferenças absolutas entre suas coordenadas. Ao contrário da distância Euclidiana, a distância de Manhattan é menos sensível a outliers, razão pela qual é adequada para tarefas de agrupamento.
Use a distância de Manhattan para considerar diferenças absolutas entre coordenadas, mas a similaridade cosseno quando a direção dos vetores é mais importante do que a magnitude.
Distância de Hamming
A distância de Hamming compara duas cadeias de dados binários de comprimento igual quantificando o número de posições de bits entre dois bits. Ela mede o número de posições onde os símbolos correspondentes de duas cadeias diferem.
A distância de Hamming é sempre um inteiro não negativo, já que a distância é a contagem total dessas discrepâncias. Tarefas de classificação em aprendizado de máquina e algoritmos de detecção de erros usam a distância de Hamming para comparar vetores binários.
Similaridade de Jaccard
A similaridade de Jaccard, também conhecida como coeficiente de Jaccard ou Índice de Jaccard, é outra medida de proximidade que calcula a similaridade entre dois vetores ou objetos binários assimétricos. Você pode calculá-la dividindo o tamanho da interseção dos conjuntos pelo tamanho da união dos conjuntos.
A similaridade de Jaccard é melhor para comparar a presença ou ausência de termos, enquanto a similaridade cosseno se destaca em medir o ângulo entre vetores em dados densos com termos sobrepostos.
Vantagens da similaridade cosseno
A principal vantagem é que a similaridade cosseno captura o aspecto direcional dos dados sem ser afetada por mudanças na magnitude do vetor. Aplicações de análise de texto, sistemas de recomendação e soluções de NLP usam a similaridade cosseno para facilitar o cálculo e reduzir eficientemente as dimensões dos vetores.
- Invariância de magnitude: A similaridade cosseno mede a direção de dois vetores e não distorce a pontuação de proximidade mesmo quando eles diferem em comprimento. Sua natureza invariante à escala a torna ideal para motores de busca e aplicações baseadas em texto, onde foca em saber se os vetores cobrem tópicos semelhantes em vez do comprimento, contagem de palavras ou verbosidade.
- Escalabilidade para dados esparsos: A similaridade cosseno usa relevância direcional para comprimir dados com grandes dimensões de forma eficiente. O resultado é um tempo de computação rápido para conjuntos de dados esparsos e de alta dimensão, tornando a similaridade cosseno ideal para bancos de dados vetoriais e sistemas de recuperação de imagens.
- Redução de dimensionalidade: A similaridade cosseno é compatível com técnicas como análise de componentes principais (PCA) e incorporação de vizinhos estocásticos distribuídos (t-SNE). Esses métodos reduzem o número de dimensões enquanto preservam a variância em um conjunto de dados. A atenção da similaridade cosseno para relações angulares garante que os pontos de dados permaneçam robustos mesmo após essas transformações mapearem vetores em um espaço de menor dimensão.
- Similaridade semântica: A pontuação de similaridade cosseno usa modelos de espaço vetorial para comparar palavras com base em seus significados em vez de contagens de palavras brutas ou similaridades sintáticas. Os principais motores de busca de banco de dados vetorial confiam nessa capacidade para medir a distância entre palavras ou sentenças vetorizadas em análise de sentimentos, modelagem de tópicos e tarefas de tradução automática.
Desvantagens da similaridade cosseno
Apesar de seus muitos benefícios, a similaridade cosseno sofre de desvantagens, incluindo:
- Maldição da dimensionalidade: A similaridade cosseno pode enfrentar desafios na análise de dados em espaços de alta dimensão, um fenômeno popularmente conhecido como a maldição da dimensionalidade. Distâncias aumentadas entre pontos de dados fazem com que os ângulos entre vetores convirjam, tornando difícil diferenciá-los usando a similaridade cosseno.
- Sensibilidade a dados esparsos: A similaridade cosseno também tem dificuldades em fornecer insights significativos em conjuntos de dados esparsos com muitas entradas zero nos vetores.
- Não considera diferença absoluta: Como a similaridade cosseno foca em um ângulo em vez da magnitude dos vetores, ela pode ignorar diferenças de magnitude, que podem transmitir informações contextuais cruciais.
- Alta dependência da representação vetorial: A similaridade cosseno pode retornar resultados imprecisos para representações vetoriais mal construídas de documentos.
Aplicações da similaridade cosseno
A similaridade cosseno é usada na recuperação de informações, mineração de texto, sistemas de recomendação, processamento de imagens, classificação de documentos e agrupamento.
“Usamos a similaridade cosseno para medir a similaridade entre o texto original e o texto gerado por IA. Isso nos ajuda a melhorar a originalidade do texto gerado por IA e personalizá-lo para a satisfação e engajamento do usuário.”
Robert Brown
Co-fundador da AI Humanize
Recuperação de informações
Sistemas de recuperação de informações como motores de busca usam a similaridade cosseno para encontrar documentos relevantes no banco de dados para consultas de busca. Essa busca por similaridade garante que os usuários obtenham documentos valiosos. Nesses casos, a incorporação de texto depende de modelos complexos de rede neural como Word2Vec, GloVe ou LLMs como GPT, BERT e LLaMa.
Sistemas de recomendação
Plataformas de streaming de filmes como a Netflix confiam na similaridade cosseno para compartilhar recomendações com base no histórico de visualização dos usuários. Esses sistemas consideram cada filme e usuário como vetores. Após gerar a incorporação vetorial usando fatoração de matriz ou autoencoders, eles usam a similaridade cosseno para recomendar filmes com base nas preferências do usuário e nos padrões de visualização passados.
Processamento de imagens
Sistemas de reconhecimento facial, aplicações de imagem médica e veículos autônomos confiam nas pontuações de similaridade cosseno para avaliar a similaridade entre imagens. Eles usam redes neurais convolucionais para gerar incorporações para imagens e capturar padrões visuais entre elas.
Dicas para usar a similaridade cosseno:
- Pré-processar dados: Considere remover palavras comuns com pouco ou nenhum valor semântico – além disso, use stemming ou lematização para reduzir palavras à sua forma base e padronizar o conjunto de dados.
- Use ponderação de termos: Empregue a técnica TF-IDF para atribuir pesos a palavras raras que aparecem frequentemente em documentos. Essa ponderação ajuda na diferenciação eficiente de vetores.
- Opte por um tamanho maior de conjunto de dados: Usar conjuntos de dados maiores permite explorar uma gama mais ampla de tópicos e estilos, facilitando a comparação de similaridades.
Eleve seu jogo de dados
O foco da similaridade cosseno em ângulos em vez de magnitude a torna ideal para recomendação de conteúdo, análise de texto, agrupamento de documentos e mineração de dados. É, sem dúvida, a melhor escolha para comparar incorporações de transformadores devido à sua natureza invariante à escala e capacidade de lidar com dados de alta dimensão. Considere o problema e os requisitos de dados para encontrar o método de cálculo de similaridade mais apropriado.
Procurando por software com arquitetura orientada a eventos para processamento de dados em tempo real? Confira as principais soluções de banco de dados analítico em tempo real.
Sagar Joshi
Sagar Joshi is a former content marketing specialist at G2 in India. He is an engineer with a keen interest in data analytics and cybersecurity. He writes about topics related to them. You can find him reading books, learning a new language, or playing pool in his free time.
