Le aziende raccolgono dati per prendere decisioni migliori.
Ma quando si fa affidamento sui dati per costruire strategie, semplificare i processi e migliorare l'esperienza del cliente, più che raccoglierli, è necessario comprenderli e analizzarli per poter trarre intuizioni preziose. L'analisi dei dati ti aiuta a studiare ciò che è già accaduto e a prevedere cosa potrebbe accadere in futuro.
L'analisi dei dati ha molti componenti e, mentre alcuni possono essere facili da comprendere e svolgere, altri sono piuttosto complessi. La buona notizia è che molti software di analisi statistica offrono intuizioni significative dai dati in pochi passaggi.
Devi comprendere i fondamenti prima di utilizzare o fare affidamento su un programma statistico per ottenere risultati accurati perché, anche se generare risultati è facile, interpretarli è un'altra storia.
Durante l'interpretazione dei dati, diventa essenziale considerare i fattori che influenzano i dati. L'analisi di regressione ti aiuta a fare proprio questo. Con l'assistenza di questo metodo di analisi statistica, puoi trovare i fattori più importanti e meno importanti in qualsiasi set di dati e capire come si relazionano.
Questa guida copre i fondamenti dell'analisi di regressione, il suo processo, i benefici e le applicazioni.
Cos'è l'analisi di regressione?
L'analisi di regressione è un processo statistico che aiuta a valutare le relazioni tra una variabile dipendente e una o più variabili indipendenti.
Lo scopo principale dell'analisi di regressione è descrivere la relazione tra variabili, ma può anche essere utilizzata per:
- Stimare il valore di una variabile utilizzando i valori noti di altre variabili.
- Prevedere risultati e cambiamenti in una variabile basandosi sulla sua relazione con altre variabili.
- Controllare l'influenza delle variabili mentre si esplora la relazione tra variabili.
Fondamenti dell'analisi di regressione
Per comprendere l'analisi di regressione in modo completo, devi costruire una conoscenza di base dei concetti statistici.
Variabili
L'analisi di regressione aiuta a identificare i fattori che influenzano le intuizioni dai dati. Puoi usarla per capire quali fattori giocano un ruolo nel creare un risultato e quanto sono significativi. Questi fattori sono chiamati variabili.
Devi comprendere due tipi principali di variabili.
- Il fattore principale su cui ti concentri è la variabile dipendente. Questa variabile è spesso misurata come un risultato delle analisi e dipende da una o più altre variabili.
- I fattori o le variabili che influenzano la tua variabile dipendente sono chiamati variabili indipendenti. Variabili come queste sono spesso modificate per l'analisi. Sono anche chiamate variabili esplicative o variabili predittive.
Correlazione vs. causalità
La causalità indica che una variabile è il risultato dell'occorrenza dell'altra variabile. La correlazione suggerisce una connessione tra variabili. Correlazione e causalità possono coesistere, ma la correlazione non implica causalità.
Overfitting
L'overfitting è un errore di modellazione statistica che si verifica quando una funzione si allinea con un set limitato di punti dati e fa previsioni basate su quelli invece di esplorare nuovi punti dati. Di conseguenza, il modello può essere utilizzato solo come riferimento al suo set di dati iniziale e non a qualsiasi altro set di dati.
Vuoi saperne di più su Software di analisi statistica? Esplora i prodotti Analisi Statistica.
Come funziona l'analisi di regressione?
Per un momento, immaginiamo che tu possieda un chiosco di gelati. In questo caso, possiamo considerare "ricavi" e "temperatura" come i due fattori sotto analisi. Il primo passo verso la conduzione di un'analisi statistica di regressione di successo è raccogliere dati sulle variabili.
Raccogli tutti i tuoi numeri di vendite mensili degli ultimi due anni e qualsiasi dato sulle variabili indipendenti o variabili esplicative che stai analizzando. In questo caso, è la temperatura media mensile degli ultimi due anni.
Per iniziare a capire se c'è una relazione tra queste due variabili, devi tracciare questi punti dati su un grafico che assomiglia al seguente esempio teorico di un diagramma a dispersione:
.png)
La quantità di vendite è rappresentata sull'asse y (asse verticale), e la temperatura è rappresentata sull'asse x (asse orizzontale). I punti rappresentano i dati di un mese: la temperatura media e le vendite in quello stesso mese.
Osservando questi dati si nota che le vendite sono più alte nei giorni in cui la temperatura aumenta. Ma di quanto? Se la temperatura aumenta, quanto vendi? E se la temperatura scende?
Tracciare una linea di regressione approssimativamente al centro di tutti i punti dati ti aiuta a capire quanto vendi tipicamente quando c'è una temperatura specifica. Usiamo un diagramma a dispersione teorico per rappresentare una linea di regressione:
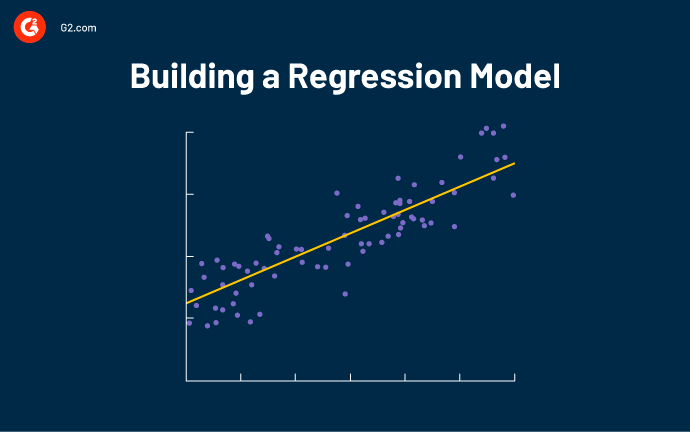
La linea di regressione spiega la relazione tra i valori previsti e le variabili dipendenti. Può essere creata utilizzando software di analisi statistica o Microsoft Excel.
Il tuo strumento di analisi di regressione deve anche mostrare una formula che definisce la pendenza della linea. Per esempio:
y = 100 + 2x + termine di errore
Osservando la formula, puoi concludere che quando non c'è x, y è uguale a 100, il che significa che quando la temperatura è molto bassa, puoi fare una media di 100 vendite. A condizione che le altre variabili rimangano costanti, puoi usare questo per prevedere il futuro delle vendite. Per ogni aumento della temperatura, fai una media di due vendite in più.
Una linea di regressione ha sempre un termine di errore perché una variabile indipendente non può essere un predittore perfetto di una variabile dipendente. Decidere se questa variabile merita la tua attenzione dipende dal termine di errore: più grande è il termine di errore, meno certa è la linea di regressione.
Tipi di analisi di regressione
Vari tipi di analisi di regressione sono a tua disposizione, ma i cinque menzionati di seguito sono i più comunemente usati.
Regressione lineare
Un modello di regressione lineare è definito come una linea retta che tenta di prevedere la relazione tra variabili. È principalmente classificato in due tipi: regressione lineare semplice e multipla.
Discuteremo di questi tra un momento, ma copriamo prima i cinque presupposti fondamentali fatti nel modello di regressione lineare.
- Le variabili dipendenti e indipendenti mostrano una relazione lineare.
- Il valore del residuo è zero.
- Il valore del residuo è costante e non correlato tra tutte le osservazioni.
- Il residuo è distribuito normalmente.
- Gli errori residui sono omoschedastici: hanno una varianza costante.
Analisi di regressione lineare semplice
L'analisi di regressione lineare aiuta a prevedere il valore di una variabile (variabile dipendente) basandosi sul valore noto di un'altra variabile (variabile indipendente).
La regressione lineare adatta una linea retta, quindi un modello lineare semplice tenta di definire la relazione tra due variabili stimando i coefficienti dell'equazione lineare.
Equazione di regressione lineare semplice:
Y = a + bX + ϵ
Dove,
Y – Variabile dipendente (variabile di risposta)
X – Variabile indipendente (variabile predittiva)
a – Intercetta (intercetta y)
b – Pendenza
ϵ – Residuo (errore)
In un tale modello di regressione lineare, una variabile di risposta ha una singola variabile predittiva corrispondente che influisce sul suo valore. Per esempio, considera la formula di regressione lineare:
y = 5x + 4
Se il valore di x è definito come 3, è possibile solo un risultato di y.
Analisi di regressione lineare multipla
Nella maggior parte dei casi, l'analisi di regressione lineare semplice non può spiegare le connessioni tra i dati. Man mano che la connessione diventa più complessa, la relazione tra i dati è meglio spiegata utilizzando più di una variabile.
L'analisi di regressione multipla descrive una variabile di risposta utilizzando più di una variabile predittiva. Viene utilizzata quando una forte correlazione tra ciascuna variabile indipendente ha la capacità di influenzare la variabile dipendente.
Equazione di regressione lineare multipla:
Y = a + bX1 + cX2 + dX3 + ϵ
Dove,
Y – Variabile dipendente
X1, X2, X3 – Variabili indipendenti
a – Intercetta (intercetta y)
b, c, d – Pendenze
ϵ – Residuo (errore)
Minimi quadrati ordinari
La regressione dei minimi quadrati ordinari stima i parametri sconosciuti in un modello. Stima i coefficienti di un'equazione di regressione lineare minimizzando la somma degli errori al quadrato tra i valori effettivi e quelli previsti configurati come una linea retta.
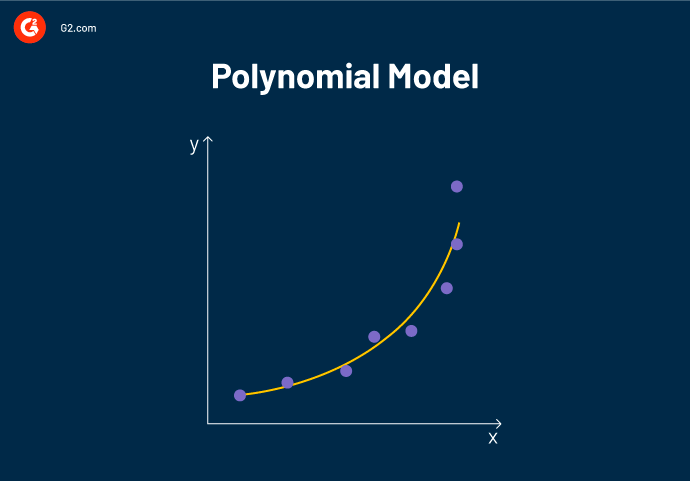
Regressione polinomiale
Un algoritmo di regressione lineare funziona solo quando la relazione tra i dati è lineare. Cosa succede se la distribuzione dei dati è più complessa, come mostrato nella figura seguente?
Come visto sopra, i dati sono non lineari. Un modello lineare non può essere utilizzato per adattare dati non lineari perché non può definire sufficientemente i modelli nei dati.
La regressione polinomiale è un tipo di regressione lineare multipla utilizzata quando i punti dati sono presenti in modo non lineare. Può determinare la relazione curvilinea tra variabili indipendenti e dipendenti che hanno una relazione non lineare.
Equazione di regressione polinomiale:
y = b0+b1x1+ b2x1^2+ b2x1^3+...... bnx1^n
Regressione logistica
La regressione logistica modella la probabilità di una variabile dipendente come funzione di variabili indipendenti. I valori di una variabile dipendente possono assumere uno di un insieme limitato di valori binari (0 e 1) poiché il risultato è una probabilità.
La regressione logistica è spesso utilizzata quando i dati binari (sì o no; passare o fallire) devono essere analizzati. In altre parole, si consiglia di utilizzare il metodo di regressione logistica per analizzare i tuoi dati se la tua variabile dipendente può avere uno dei due valori binari.
Supponiamo che tu debba determinare se un'email è spam. Dobbiamo impostare una soglia in base alla quale può essere effettuata la classificazione. Utilizzare la regressione logistica qui ha senso poiché il risultato è strettamente limitato ai valori 0 (spam) o 1 (non spam).
Regressione lineare bayesiana
In altri metodi di regressione, l'output è derivato da uno o più attributi. Ma cosa succede se quegli attributi non sono disponibili?
Il metodo di regressione bayesiana viene utilizzato quando il set di dati che deve essere analizzato ha dati scarsi o distribuiti male perché il suo output è derivato da una distribuzione di probabilità invece che da stime puntuali. Quando i dati sono assenti, puoi posizionare un prior sui coefficienti di regressione per sostituire i dati. Man mano che aggiungiamo più punti dati, l'accuratezza del modello di regressione migliora.
Immagina che un'azienda lanci un nuovo prodotto e voglia prevederne le vendite. A causa della mancanza di dati disponibili, non possiamo utilizzare un semplice modello di analisi di regressione. Ma l'analisi di regressione bayesiana ti consente di impostare un prior e calcolare proiezioni future.
Inoltre, una volta che arrivano nuovi dati dalle vendite del nuovo prodotto, il prior viene immediatamente aggiornato. Di conseguenza, la previsione per il futuro è influenzata dai dati più recenti e precedenti.
La tecnica bayesiana è matematicamente robusta. Per questo motivo, non richiede di avere alcuna conoscenza preliminare del set di dati durante l'uso. Tuttavia, la sua complessità significa che ci vuole tempo per trarre inferenze dal modello, e usarlo non ha senso quando hai troppi dati.
Analisi di regressione quantile
Il metodo di regressione lineare stima la media di una variabile basandosi sui valori di altre variabili predittive. Ma non sempre abbiamo bisogno di calcolare la media condizionale. Nella maggior parte delle situazioni, abbiamo solo bisogno della mediana, del quantile 0,25, e così via. In casi come questo, possiamo usare la regressione quantile.
La regressione quantile definisce la relazione tra una o più variabili predittive e specifici percentili o quantili di una variabile di risposta. Resiste all'influenza delle osservazioni fuori scala. Non vengono fatte ipotesi sulla distribuzione della variabile dipendente nella regressione quantile, quindi puoi usarla quando la regressione lineare non soddisfa le sue ipotesi.
Consideriamo due studenti che hanno sostenuto un esame di Olimpiadi aperto a tutte le fasce d'età. Lo studente A ha ottenuto 650, mentre lo studente B ha ottenuto 425. Questi dati mostrano che lo studente A ha performato meglio dello studente B.
Ma la regressione quantile ci aiuta a ricordare che poiché l'esame era aperto a tutte le fasce d'età, dobbiamo considerare l'età dello studente per determinare il risultato corretto nei loro spazi quantili condizionali individuali.
Sappiamo quale variabile causa una tale differenza nella distribuzione dei dati. Di conseguenza, i punteggi degli studenti vengono confrontati per le stesse fasce d'età.
Cos'è la regolarizzazione?
La regolarizzazione è una tecnica che impedisce a un modello di regressione di overfitting includendo informazioni extra. Viene implementata aggiungendo un termine di penalità al modello di dati. Ti consente di mantenere lo stesso numero di caratteristiche riducendo l'entità delle variabili. Riduce l'entità del coefficiente delle caratteristiche verso zero.
I due tipi di tecniche di regolarizzazione sono L1 e L2. Un modello di regressione che utilizza la tecnica di regolarizzazione L1 è noto come regressione Lasso, e quello che utilizza la tecnica di regolarizzazione L2 è chiamato regressione Ridge.
Regressione Ridge
La regressione Ridge è una tecnica di regolarizzazione che utilizzeresti per eliminare le correlazioni tra variabili indipendenti (multicollinearità) o quando il numero di variabili indipendenti in un set supera il numero di osservazioni.
La regressione Ridge esegue la regolarizzazione L2. In una tale regolarizzazione, la formula utilizzata per fare previsioni è la stessa dei minimi quadrati ordinari, ma viene aggiunta una penalità al quadrato dell'entità dei coefficienti di regressione. Questo viene fatto in modo che ogni caratteristica abbia il minor effetto possibile sul risultato.
Regressione Lasso
Lasso sta per Least Absolute Shrinkage and Selection Operator.
La regressione Lasso è una regressione lineare regolarizzata che utilizza una penalità L1 che spinge alcuni valori dei coefficienti di regressione a diventare più vicini a zero. Impostando le caratteristiche a zero, sceglie automaticamente la caratteristica richiesta ed evita l'overfitting.
Quindi, se il set di dati ha alta correlazione, alti livelli di multicollinearità, o quando specifiche caratteristiche come la selezione delle variabili o l'eliminazione dei parametri devono essere automatizzate, puoi usare la regressione Lasso.
Ora è il momento di ricevere notizie e intrattenimento SaaS-y con la nostra newsletter di 5 minuti, G2 Tea, con leader ispiratori, opinioni audaci e previsioni coraggiose. Iscriviti oggi!
Quando viene utilizzata l'analisi di regressione?
L'analisi di regressione è uno strumento potente utilizzato per derivare inferenze statistiche per il futuro utilizzando osservazioni del passato. Identifica le connessioni tra variabili che si verificano in un set di dati e determina l'entità di queste associazioni e la loro importanza sui risultati.
In tutti i settori, è uno strumento di analisi statistica utile perché offre un'eccezionale flessibilità. Quindi, la prossima volta che qualcuno al lavoro propone un piano che dipende da più fattori, esegui un'analisi di regressione per prevedere un risultato accurato.
Benefici dell'analisi di regressione
Nel mondo reale, vari fattori determinano come cresce un'azienda. Spesso questi fattori sono interconnessi, e un cambiamento in uno può influenzare positivamente o negativamente l'altro.
Utilizzare l'analisi di regressione per giudicare come le variabili in cambiamento influenzeranno la tua azienda ha due benefici principali.
- Prendere decisioni basate sui dati: Le aziende utilizzano l'analisi di regressione quando pianificano per il futuro perché aiuta a determinare quali variabili hanno l'impatto più significativo sul risultato secondo i risultati precedenti. Le aziende possono concentrarsi meglio sulle cose giuste quando fanno previsioni e prendono decisioni basate sui dati.
- Riconoscere le opportunità di miglioramento: Poiché l'analisi di regressione mostra le relazioni tra due variabili, le aziende possono usarla per identificare aree di miglioramento in termini di persone, strategie o strumenti osservando le loro interazioni. Per esempio, aumentare il numero di persone su un progetto potrebbe avere un impatto positivo sulla crescita dei ricavi.
Applicazioni dell'analisi di regressione
Sia le piccole che le grandi industrie sono cariche di una quantità enorme di dati. Per prendere decisioni migliori ed eliminare le congetture, molte stanno ora adottando l'analisi di regressione perché offre un approccio scientifico alla gestione.
Utilizzando l'analisi di regressione, i professionisti possono osservare e valutare la relazione tra varie variabili e successivamente prevedere le caratteristiche future di questa relazione.
Le aziende possono utilizzare l'analisi di regressione in numerose forme. Alcune di esse:
- Molti professionisti della finanza utilizzano l'analisi di regressione per prevedere opportunità e rischi futuri. Il modello di pricing degli asset di capitale (CAPM) che decide la relazione tra il rendimento atteso di un asset e il premio di rischio di mercato associato è un modello di regressione spesso utilizzato in finanza per il pricing degli asset e la scoperta dei costi del capitale. L'analisi di regressione è anche utilizzata per calcolare il beta (β), che è descritto come la volatilità dei rendimenti considerando il mercato complessivo per un'azione.
- Le compagnie assicurative utilizzano l'analisi di regressione per prevedere l'affidabilità creditizia di un assicurato. Può anche aiutare a scegliere il numero di richieste che possono essere sollevate in un periodo specifico.
- La previsione delle vendite utilizza l'analisi di regressione per prevedere le vendite basandosi sulle prestazioni passate. Può darti un'idea di cosa ha funzionato prima, che tipo di impatto ha creato e cosa può migliorare per fornire risultati futuri più accurati e vantaggiosi.
- Un altro uso critico dei modelli di regressione è l'ottimizzazione dei processi aziendali. Oggi, i manager considerano la regressione uno strumento indispensabile per evidenziare le aree che hanno il massimo impatto sull'efficienza operativa e sui ricavi, derivare nuove intuizioni e correggere errori di processo.
I migliori software di analisi statistica
Le aziende con una cultura basata sui dati utilizzano l'analisi di regressione per trarre intuizioni azionabili da grandi set di dati. Per molte industrie leader con ampi cataloghi di dati, si dimostra essere un asset prezioso. Man mano che la dimensione dei dati aumenta, ulteriori dirigenti si affidano all'analisi di regressione per prendere decisioni aziendali informate con significatività statistica.
Mentre Microsoft Excel rimane uno strumento popolare per condurre un'analisi dei dati di regressione fondamentale, molti strumenti statistici più avanzati oggi forniscono risultati più accurati e veloci. Scopri i migliori software di analisi statistica nel 2023 qui.
Per essere inclusi in questa categoria, il prodotto software di analisi di regressione deve essere in grado di:
- Eseguire una regressione lineare semplice o un'analisi di regressione multipla complessa per vari set di dati.
- Fornire strumenti grafici per studiare la stima del modello, la multicollinearità, l'adattamento del modello, la linea di miglior adattamento e altri aspetti tipici del tipo di regressione.
- Possedere un design dell'interfaccia utente (UI) pulito, intuitivo e facile da usare
*Di seguito sono riportate le 5 principali soluzioni software di analisi statistica leader dal Winter 2023 Grid® Report di G2. Alcune recensioni possono essere modificate per chiarezza.
1. IBM SPSS statistics
IBM SPSS Statistics ti consente di prevedere i risultati e applicare varie procedure di regressione non lineare che possono essere utilizzate per progetti aziendali e di analisi in cui le tecniche di regressione standard sono limitanti o inadeguate. Con IBM SPSS Statistics, puoi specificare più modelli di regressione in un unico comando per osservare la correlazione tra variabili indipendenti e dipendenti ed espandere le capacità di analisi di regressione su un set di dati.
Cosa piace di più agli utenti:
"Ho usato un paio di diversi software statistici. IBM SPSS è un software straordinario, un negozio unico per tutte le analisi relative alle statistiche. L'interfaccia utente grafica è elegantemente costruita per facilità. Sono stato in grado di imparare e usarlo rapidamente"
- Recensione di IBM SPSS Statistics, Haince Denis P.
Cosa non piace agli utenti:
"Alcune delle interfacce potrebbero essere più intuitive. Fortunatamente, molte informazioni sono disponibili da varie fonti online per aiutare l'utente a imparare come impostare i test."
- Recensione di IBM SPSS Statistics, David I.
2. Posit
Per rendere la scienza dei dati più intuitiva e collaborativa, Posit fornisce agli utenti di settori chiave strumenti basati su R e Python, consentendo loro di sfruttare potenti analisi e raccogliere intuizioni preziose.
Cosa piace di più agli utenti:
"Sintassi semplice, eccellenti funzioni integrate e potenti librerie per tutto il resto. Costruire qualsiasi cosa, da semplici funzioni matematiche a modelli di apprendimento automatico complicati, è un gioco da ragazzi."
- Recensione di Posit, Brodie G.
Cosa non piace agli utenti:
"La sua GUI potrebbe essere più intuitiva e user-friendly. Ci vuole molto tempo per capire e implementare. Includere un gestore di pacchetti sarebbe una buona idea, poiché è diventato comune in molti IDE moderni. Deve esserci un'opzione per salvare i comandi della console, che attualmente non è disponibile."
- Recensione di Posit, Tanishq G.
3. JMP
JMP è un software di analisi dei dati che aiuta a dare un senso ai tuoi dati utilizzando metodi statistici all'avanguardia e moderni. I suoi prodotti sono intuitivamente interattivi, visivamente accattivanti e statisticamente profondi.
Cosa piace di più agli utenti:
"I video istruttivi sul sito web sono fantastici; non avevo idea di cosa stessi facendo prima di guardarli. I video rendono l'applicazione molto user-friendly."
- Recensione di JMP, Ashanti B.
Cosa non piace agli utenti:
"La funzione di aiuto può essere breve in termini di ciò che comporta la funzionalità, e questo è deludente perché il modo in cui il software è impostato per comunicare i dati visivamente e intuitivamente suggerisce la presenza di un processo di pensiero scientifico logico e spiegabile, inclusa una spiegazione del "perché". Il costruttore di grafici potrebbe anche utilizzare mezzi più intuitivi per cambiare le caratteristiche del layout."
- Recensione di JMP, Zeban K.
4. Software statistico Minitab
Software statistico Minitab è uno strumento di analisi dei dati e statistica utilizzato per aiutare le aziende a comprendere i loro dati e prendere decisioni migliori. Consente alle aziende di sfruttare il potere dell'analisi di regressione analizzando dati nuovi e vecchi per scoprire tendenze, prevedere modelli, scoprire relazioni nascoste tra variabili e creare visualizzazioni sorprendenti.
Cosa piace di più agli utenti:
"Il miglior programma per imparare e analizzare poiché ti consente di migliorare le impostazioni con grafici e diagrammi di regressione incredibilmente accurati. Questa piattaforma ti consente di analizzare i risultati o i dati con i loro valori ideali."
- Recensione del software statistico Minitab, Pratibha M.
Cosa non piace agli utenti:
"Il prezzo del software è elevato e la licenza è problematica. È necessario essere online o connessi alla VPN aziendale per la licenza, soprattutto per l'uso aziendale. Quindi, senza una connessione internet, non puoi usarlo affatto. Inoltre, se sei nel mezzo di un'analisi e perdi la connessione internet, rischi di perdere il progetto o lo studio su cui stai lavorando."
- Recensione del software statistico Minitab, Siew Kheong W.
5. EViews
EViews offre strumenti user-friendly per eseguire la modellazione dei dati e le previsioni. Opera con un'interfaccia innovativa e facile da usare orientata agli oggetti utilizzata da ricercatori, istituzioni finanziarie, agenzie governative ed educatori.
Cosa piace di più agli utenti:
"Come economista, questo software è utile poiché mi assiste nel condurre ricerche avanzate, analizzare dati e interpretare risultati per raccomandazioni politiche. Non posso fare a meno di EViews. Mi piacciono i suoi aggiornamenti recenti che hanno anche migliorato l'interfaccia utente."
- Recensione di EViews, Thomas M.
Cosa non piace agli utenti:
"Nella mia esperienza, importare dati da Excel non è facile usando EViews rispetto ad altri software statistici. È necessario sviluppare competenze mentre si importano dati in EViews da diversi formati. Inoltre, il prezzo del software è molto alto."
- Recensione di EViews, Md. Zahid H.
Raccogliere dati non raccoglie muschio.
La raccolta dei dati è diventata facile nel mondo moderno, ma più che raccogliere è necessario. Le aziende devono sapere come ottenere il massimo valore da questi dati. L'analisi aiuta le aziende a comprendere le informazioni disponibili, trarre intuizioni azionabili e prendere decisioni informate. Le aziende dovrebbero conoscere a fondo il processo di analisi dei dati per perfezionare le operazioni, migliorare il servizio clienti e monitorare le prestazioni.
Scopri di più sui vari stadi del processo di analisi dei dati e implementali per guidare il successo.

Devyani Mehta
Devyani Mehta is a content marketing specialist at G2. She has worked with several SaaS startups in India, which has helped her gain diverse industry experience. At G2, she shares her insights on complex cybersecurity concepts like web application firewalls, RASP, and SSPM. Outside work, she enjoys traveling, cafe hopping, and volunteering in the education sector. Connect with her on LinkedIn.


