Imagina esto: estás comprando en línea una laptop de alto rendimiento.
Haces clic en una, y aparecen varias sugerencias similares. Están cerca de lo que buscas pero no son lo mismo. ¿Cómo sabe el sitio web cuáles son relevantes para tu búsqueda?
Aquí es donde entra en juego la similitud del coseno, una herramienta matemática que mide la similitud entre dos vectores no nulos en un espacio de alta dimensión.
Las bases de datos vectoriales en motores de búsqueda y sistemas de recomendación utilizan la similitud del coseno para entender qué tan estrechamente coinciden los productos o consultas de búsqueda en una base de datos basándose en sus representaciones vectoriales. Comprender estas relaciones y patrones entre los elementos permite a las soluciones de bases de datos vectoriales recuperar sugerencias personalizadas y precisas que te mantienen navegando, y tal vez incluso comprando.
¿Qué es la similitud del coseno?
La similitud del coseno es una métrica matemática que mide la similitud entre dos vectores en un espacio de producto interno o multidimensional. Utiliza el coseno del ángulo entre dos vectores para determinar si apuntan en la misma dirección, independientemente de sus magnitudes.
En otras palabras, la similitud del coseno es el producto escalar o punto de dos vectores dividido por el producto de sus magnitudes. También se conoce como similitud de Orchini y coeficiente de congruencia de Tucker.
Científicos de datos, ingenieros de aprendizaje automático y desarrolladores de software utilizan la similitud del coseno para comparar miles de puntos de datos y entender sus relaciones sin perderse en los detalles. Se utiliza ampliamente para medir la similitud en minería de texto, recuperación de información y aplicaciones de análisis de texto.
Otras medidas de similitud populares incluyen la distancia euclidiana, la distancia de Manhattan, la similitud de Jaccard y la distancia de Minkowski.
¿Por qué es importante la similitud del coseno?
La similitud del coseno proporciona una forma robusta de evaluar la similitud semántica entre documentos, conjuntos de datos e imágenes de alta dimensión y dispersos. Es efectiva porque se centra en la orientación de dos vectores en un espacio, midiendo su similitud independientemente de su magnitud.
Las aplicaciones de análisis de texto que utilizan la frecuencia de término-inversa frecuencia de documento (TF-IDF), Word2Vec y representaciones de codificadores bidireccionales de transformadores (BERT) derivan vectores de palabras con grandes dimensiones pero bajo solapamiento. Las métricas de similitud tradicionales como la distancia euclidiana son sensibles a las longitudes de los vectores y no pueden manejar estos vectores. La similitud del coseno puede centrarse fácilmente en la correlación de datos en tales escenarios.
La similitud del coseno también ayuda a las aplicaciones de recuperación de información a clasificar documentos basándose en qué tan bien coinciden con una consulta, incluso cuando los documentos varían en longitud o complejidad.
La escalabilidad de la similitud del coseno en el espacio vectorial de alta dimensión la hace invaluable para las bases de datos vectoriales, donde encontrar vecinos más cercanos de manera rápida y precisa es necesario para la recuperación de imágenes, sistemas de recomendación y detección de anomalías.
El procesamiento del lenguaje natural (NLP) depende de la similitud del coseno para comparar eficientemente incrustaciones vectoriales. Esta comparación de incrustaciones ayuda a los algoritmos de NLP a clasificar, agrupar o recomendar contenido basándose en la similitud semántica de los documentos.
¿Quieres aprender más sobre Software de base de datos vectorial? Explora los productos de Base de datos vectorial.
¿Cómo funciona la similitud del coseno?
La similitud del coseno cuantifica la similitud entre dos vectores calculando el coseno del ángulo entre ellos. A continuación se detalla cómo funciona la similitud del coseno en entornos de datos dispersos y de alta dimensión.
- Representación vectorial: El primer paso implica convertir objetos como palabras, documentos, imágenes o textos en vectores en un espacio de alta dimensión. Cada dimensión del vector representa un solo objeto, con su valor mostrando la frecuencia del vector o su importancia.
- Producto escalar: El producto escalar cuantifica la relación entre dos vectores multiplicando sus componentes correspondientes y sumando los resultados. Calcular este producto escalar es vital para entender la alineación entre vectores en la misma dirección.
- Cálculo de magnitud: El siguiente paso implica calcular las longitudes o magnitudes de cada vector.
- Similitud del coseno: La puntuación de similitud del coseno es el producto escalar dividido por el producto de las magnitudes de los dos vectores.
Dividir el producto escalar por el producto de las magnitudes de los vectores normaliza el resultado de similitud a un rango entre -1 y 1. Esta normalización asegura que la puntuación de similitud refleje solo el ángulo de orientación de los vectores, no su magnitud. Mide consistentemente la similitud de los vectores, independientemente de la escala de los datos.
Cómo calcular la similitud del coseno
Calcular la similitud del coseno requiere encontrar el producto escalar de dos vectores. Luego, multiplica las magnitudes de esos dos vectores. Ahora, divide el producto escalar por el producto de las magnitudes para encontrar la puntuación de similitud del coseno.
Fórmula de similitud del coseno
La puntuación de similitud del coseno entre dos vectores, A y B, se calcula usando la fórmula a continuación:
Similitud del Coseno (A, B) = (A·B) / (||A|| * ||B||)
Dónde,
A · B es el producto escalar de los vectores A y B
||A|| y ||B|| representan la longitud o magnitud de los dos vectores A y B
||A|| * ||B|| denota el producto de las magnitudes de los vectores A y B
La similitud del coseno varía entre -1 y 1.
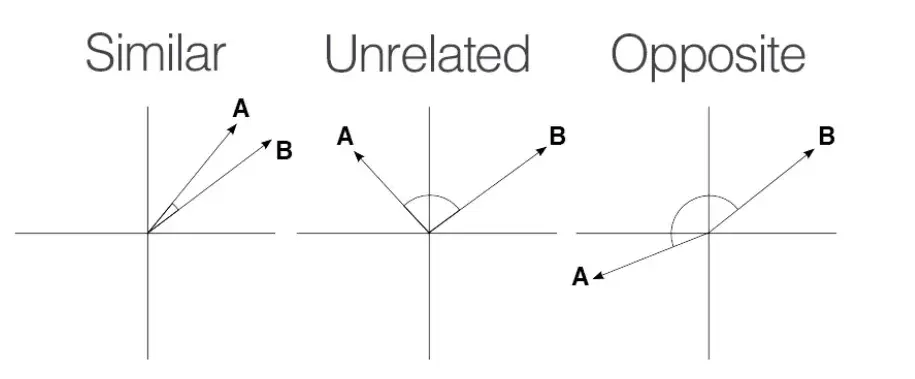Fuente: Medium
Una puntuación de 1 significa que los vectores están perfectamente alineados o son proporcionales, indicando máxima similitud.
Una puntuación de 0 implica que los vectores son ortogonales, lo que significa que no tienen similitud.
Una puntuación de -1 muestra que los vectores son perfectamente opuestos, lo que significa que apuntan en direcciones opuestas pero tienen la misma magnitud.
Ejemplo de similitud del coseno
Calculemos la similitud del coseno entre los vectores A y B.
El vector A tiene valores, A = { 1, 9, 3, 6 } El vector ‘B’ tiene valores, B = { 1, 7, 0, 1 }
Producto escalar: A·B = 1×1 + 9×7 + 3×0 + 6×1 =70
Magnitud de A: ||A|| = √(1² + 9² + 3² + 6²) = √(1 + 81 + 9 + 36) = √127 ≈ 11.27
Magnitud de B: ||B|| = √(1² + 7² + 0² + 1²) = √(1 + 49 + 0 + 1) = √51 ≈ 7.14
Similitud del Coseno = (A · B) / (||A|| * ||B||) = 70 / (11.27 × 7.14) ≈ 0.87
La similitud del coseno entre los vectores A y B es aproximadamente 0.87, lo que muestra una similitud sustancial entre ellos.
Bibliotecas para el cálculo de la similitud del coseno
Calcular la similitud del coseno es sencillo pero puede ser difícil cuando se trabaja con grandes conjuntos de datos. En tales situaciones, puedes usar lenguajes de programación como Python y bibliotecas y herramientas como Matlab, SciKit-Learn, TensorFlow y SciPy.
NumPy
NumPy es una poderosa biblioteca de Python para cálculos numéricos. Soporta operaciones de matrices multidimensionales, matrices y funciones matemáticas, lo que la hace ideal para cálculos de similitud del coseno.
Cómo calcular la similitud del coseno usando NumPy
# importar bibliotecas requeridas
import numpy as np
from numpy.linalg import norm
# definir dos listas o matrices
A = np.array([1, 9, 3, 6])
B = np.array([1, 7, 0, 1])
print("A:", A)
print("B:", B)
# calcular similitud del coseno
cosine = np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B))
print("Similitud del Coseno:", cosine)
SciKit-Learn
SciKit-Learn es una biblioteca de aprendizaje automático basada en Python con funciones integradas para tareas de análisis de datos, incluida la similitud del coseno. El módulo sklearn.metrics.pairwise ofrece una función de cosine_similarity para manejar tanto matrices densas como dispersas.
Cómo calcular la similitud del coseno usando SciKit-Learn
# importar bibliotecas requeridas
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
# definir los vectores
A = np.array([[1, 9, 3, 6]])
B = np.array([[1, 7, 0, 1]])
# calcular similitud del coseno
cosine_sim = cosine_similarity(A, B)
print("Similitud del Coseno:", cosine_sim[0][0])
SciPy
SciPy es otra popular biblioteca basada en Python para la computación científica. Construida sobre NumPy, SciPy cuenta con funciones optimizadas que calculan la similitud del coseno para grandes conjuntos de datos. Su módulo scipy.spatial.distance incluye una función de cálculo de distancia del coseno, que puedes usar para calcular la similitud del coseno.
Cómo calcular la similitud del coseno usando SciPy
# importar bibliotecas requeridas
import numpy as np
from scipy.spatial.distance import cosine
# definir los vectores
A = np.array([1, 9, 3, 6])
B = np.array([1, 7, 0, 1])
# calcular distancia del coseno
cosine_distance = cosine(A, B)
# calcular similitud del coseno
cosine_similarity = 1 - cosine_distance
print("Similitud del Coseno:", cosine_similarity)
Gensim
Gensim es una biblioteca de Python ampliamente utilizada para modelado de temas y procesamiento del lenguaje natural. Cuenta con funciones integradas para calcular la similitud del coseno entre un gran volumen de documentos de texto y vectores de palabras.
Cómo calcular la similitud del coseno usando Gensim
# importar bibliotecas requeridas
from gensim import corpora
from gensim.matutils import sparse2full
from gensim.similarities import MatrixSimilarity
from gensim.models import TfidfModel
import numpy as np
# documentos de muestra
documents = [
"Me encanta jugar al fútbol.",
"El fútbol es un gran deporte.",
"Disfruto viendo películas.",
"Las películas son entretenidas.",
]
# tokenizar y preprocesar
texts = [[word.lower() for word in doc.split()] for doc in documents]
# crear un diccionario y corpus
dictionary = corpora.Dictionary(texts)
corpus = [dictionary.doc2bow(text) for text in texts]
# crear un modelo TF-IDF
tfidf_model = TfidfModel(corpus)
tfidf_corpus = tfidf_model[corpus]
# crear un índice de similitud
index = MatrixSimilarity(tfidf_corpus)
# calcular la similitud del primer documento con todos los demás
similarities = index[tfidf_corpus[0]]
# imprimir las similitudes
print("Similitudes del Coseno para el Documento 0:", similarities)
TensorFlow y PyTorch
TensorFlow y PyTorch son bibliotecas populares de aprendizaje profundo que ayudan a medir la similitud entre vectores de características de alta dimensión.
Cómo calcular la similitud del coseno usando TensorFlow
# importar bibliotecas requeridas
import tensorflow as tf
# definir los vectores
A = tf.constant([1.0, 9.0, 3.0, 6.0])
B = tf.constant([1.0, 7.0, 0.0, 1.0])
# calcular similitud del coseno
def cosine_similarity(A, B):
# calcular el producto escalar
dot_product = tf.reduce_sum(A * B)
# calcular la norma (magnitud) de los vectores
norm_A = tf.sqrt(tf.reduce_sum(tf.square(A)))
norm_B = tf.sqrt(tf.reduce_sum(tf.square(B)))
# calcular similitud del coseno
cosine_sim = dot_product / (norm_A * norm_B)
return cosine_sim
similarity = cosine_similarity(A, B)
print("Similitud del Coseno:", similarity.numpy())
# calcular similitud del coseno
cosine_similarity = 1 - cosine_distance
print("Similitud del Coseno:", cosine_similarity)
Al usar PyTorch, los desarrolladores pueden usar torch.tensor() para crear objetos tensoriales y usar la función torch.norm() para calcular la norma euclidiana de los vectores.
Considera usar los siguientes consejos para optimizar los cálculos de coseno en Python:
- Opta por bibliotecas optimizadas. Usa las operaciones vectorizadas de NumPy o SciKit-Learn para calcular la similitud del coseno y reducir la sobrecarga de los bucles de Python. Estas bibliotecas también funcionan más rápido que el Python básico.
- Usa Numba. Numba es un compilador de tiempo de ejecución (JIT) de código abierto para código Python y NumPy. Te ayuda a paralelizar automáticamente los cálculos de similitud del coseno usando múltiples unidades de procesamiento central (CPU).
- Emplea matrices dispersas. Considera usar las representaciones de matrices dispersas de SciPy al manejar conjuntos de datos con múltiples valores cero. Te ayudará a ahorrar memoria y tiempo de cálculo para tareas de análisis de similitud de texto y documentos.
- Usa Cython para la compilación de código. Cython permite a los desarrolladores escribir códigos similares a C con una sintaxis similar a Python. Usarlo para la compilación de código les ayuda a lograr velocidades similares a C o C++ mientras mantienen la facilidad de la sintaxis de Python.
- Usa algoritmos ANN. Los algoritmos de vecinos más cercanos aproximados o ANN como KD-Tress o el hash sensible a la localidad (LSH) ayudan a encontrar vectores similares sin calcular la similitud del coseno. Estos algoritmos pueden ser beneficiosos para aplicaciones a gran escala.
- Accede a GPUs. Usar unidades de procesamiento gráfico o GPUs con bibliotecas de Python como TensorFlow también puede ayudar a lograr un mayor rendimiento al trabajar con conjuntos de datos extensos y de alta dimensión.
Similitud del coseno vs. otros métodos para el cálculo de similitud
La similitud del coseno no es el único método para medir la similitud entre objetos en un conjunto de datos. Otros métodos populares de cálculo de similitud son:
Distancia euclidiana
La distancia euclidiana mide la distancia en línea recta entre dos puntos en el espacio euclidiano. Siempre es cero o positiva. Puede que no puedas encontrar una distancia euclidiana significativa en espacios de alta dimensión ya que los puntos tienden a converger.
La similitud del coseno es ideal para datos de alta dimensión o análisis de texto donde la magnitud del vector no es esencial. La similitud euclidiana funciona mejor para espacios de menor dimensión donde la magnitud del vector es vital.
Distancia de Manhattan
Esta mide la distancia entre dos puntos en un camino similar a una cuadrícula sumando las diferencias absolutas entre sus coordenadas. A diferencia de la distancia euclidiana, la distancia de Manhattan es menos sensible a los valores atípicos, por lo que es adecuada para tareas de agrupamiento.
Usa la distancia de Manhattan para considerar diferencias absolutas entre coordenadas pero la similitud del coseno cuando la dirección de los vectores es más importante que la magnitud.
Distancia de Hamming
La distancia de Hamming compara dos cadenas de datos binarias de igual longitud cuantificando el número de posiciones de bits entre dos bits. Mide el número de posiciones donde los símbolos correspondientes de dos cadenas difieren.
La distancia de Hamming siempre es un entero no negativo ya que la distancia es el conteo total de estas discrepancias. Las tareas de clasificación en aprendizaje automático y los algoritmos de detección de errores usan la distancia de Hamming para comparar vectores binarios.
Similitud de Jaccard
La similitud de Jaccard, también conocida como coeficiente de Jaccard o índice de Jaccard, es otra medida de proximidad que calcula la similitud entre dos vectores binarios asimétricos u objetos. Puedes calcularla dividiendo el tamaño de la intersección de conjuntos por el tamaño de la unión de conjuntos.
La similitud de Jaccard es mejor para comparar la presencia o ausencia de términos, mientras que la similitud del coseno sobresale en medir el ángulo entre vectores en datos densos con términos superpuestos.
Ventajas de la similitud del coseno
La principal ventaja es que la similitud del coseno captura el aspecto direccional de los datos sin verse afectada por cambios en la magnitud del vector. Las aplicaciones de análisis de texto, sistemas de recomendación y soluciones de NLP usan la similitud del coseno para facilitar el cálculo y reducir eficientemente las dimensiones del vector.
- Invariancia de magnitud: La similitud del coseno mide la dirección de dos vectores y no sesga la puntuación de proximidad incluso cuando difieren en longitud. Su naturaleza invariante a la escala la hace ideal para motores de búsqueda y aplicaciones basadas en texto, donde se centra en si los vectores cubren temas similares en lugar de la longitud, el conteo de palabras o la verbosidad.
- Escalabilidad para datos dispersos: La similitud del coseno utiliza la relevancia direccional para comprimir eficientemente datos con grandes dimensiones. El resultado es un tiempo de cálculo rápido para conjuntos de datos dispersos y de alta dimensión, lo que hace que la similitud del coseno sea ideal para bases de datos vectoriales y sistemas de recuperación de imágenes.
- Reducción de dimensionalidad: La similitud del coseno es compatible con técnicas como el análisis de componentes principales (PCA) y la incrustación de vecinos estocásticos distribuidos (t-SNE). Estos métodos reducen el número de dimensiones mientras preservan la varianza en un conjunto de datos. La atención de la similitud del coseno a las relaciones angulares asegura que los puntos de datos permanezcan robustos incluso después de que estas transformaciones mapeen vectores en un espacio de menor dimensión.
- Similitud semántica: La puntuación de similitud del coseno utiliza modelos de espacio vectorial para comparar palabras basándose en sus significados en lugar de conteos de palabras en bruto o similitudes sintácticas. Los mejores motores de búsqueda de bases de datos vectoriales confían en esta capacidad para medir la distancia entre palabras o frases vectorizadas en tareas de análisis de sentimientos, modelado de temas y traducción automática.
Desventajas de la similitud del coseno
A pesar de sus muchos beneficios, la similitud del coseno sufre desventajas, incluyendo:
- La maldición de la dimensionalidad: La similitud del coseno puede enfrentar desafíos en analizar datos en espacios de alta dimensión, un fenómeno conocido popularmente como la maldición de la dimensionalidad. Las distancias aumentadas entre puntos de datos hacen que los ángulos entre vectores converjan, dificultando diferenciarlos usando la similitud del coseno.
- Sensibilidad a datos dispersos: La similitud del coseno también tiene dificultades para proporcionar información significativa en conjuntos de datos dispersos con muchas entradas cero en los vectores.
- No considera la diferencia absoluta: Como la similitud del coseno se centra en un ángulo en lugar de la magnitud de los vectores, puede pasar por alto diferencias de magnitud, que pueden transmitir información contextual crucial.
- Alta dependencia de la representación vectorial: La similitud del coseno puede devolver resultados inexactos para representaciones vectoriales mal construidas de documentos.
Aplicaciones de la similitud del coseno
La similitud del coseno se utiliza en la recuperación de información, minería de texto, sistemas de recomendación, procesamiento de imágenes, clasificación de documentos y agrupamiento.
“Usamos la similitud del coseno para medir la similitud entre el texto original y el texto generado por IA. Nos ayuda a mejorar la originalidad del texto generado por IA y personalizarlo para la satisfacción y el compromiso del usuario.”
Robert Brown
Co-fundador de AI Humanize
Recuperación de información
Los sistemas de recuperación de información como los motores de búsqueda utilizan la similitud del coseno para encontrar documentos relevantes en la base de datos para consultas de búsqueda. Esta búsqueda de similitud asegura que los usuarios obtengan documentos valiosos. En estos casos, la incrustación de texto se basa en modelos complejos de redes neuronales como Word2Vec, GloVe o LLMs como GPT, BERT y LLaMa.
Sistemas de recomendación
Plataformas de transmisión de películas como Netflix confían en la similitud del coseno para compartir recomendaciones basadas en el historial de visualización de los usuarios. Estos sistemas consideran cada película y usuario como vectores. Después de generar incrustaciones vectoriales usando la factorización de matrices o autoencoders, utilizan la similitud del coseno para recomendar películas basadas en las preferencias del usuario y los patrones de visualización pasados.
Procesamiento de imágenes
Los sistemas de reconocimiento facial, las aplicaciones de imágenes médicas y los vehículos autónomos confían en las puntuaciones de similitud del coseno para evaluar la similitud entre imágenes. Utilizan redes neuronales convolucionales para generar incrustaciones para imágenes y capturar patrones visuales entre ellas.
Consejos para usar la similitud del coseno:
- Preprocesar datos: Considera eliminar palabras comunes sin valor semántico, también usa la derivación o lematización para reducir las palabras a su forma base y estandarizar el conjunto de datos.
- Usar ponderación de términos: Emplea la técnica TF-IDF para asignar pesos a palabras raras que aparecen frecuentemente en documentos. Esta ponderación ayuda en la diferenciación eficiente de vectores.
- Optar por un tamaño de conjunto de datos más grande: Usar conjuntos de datos más grandes te permite explorar una gama más amplia de temas y estilos, lo que facilita la comparación de similitudes.
Mejora tu juego de datos
El enfoque de la similitud del coseno en los ángulos en lugar de la magnitud la hace ideal para la recomendación de contenido, análisis de texto, agrupamiento de documentos y minería de datos. Sin duda, es la mejor opción para comparar incrustaciones de transformadores debido a su naturaleza invariante a la escala y su capacidad para manejar datos de alta dimensión. Considera el problema y los requisitos de datos para encontrar el método de cálculo de similitud más apropiado.
¿Buscas software con arquitectura impulsada por eventos para el procesamiento de datos en tiempo real? Consulta las mejores soluciones de bases de datos analíticas en tiempo real.
Sagar Joshi
Sagar Joshi is a former content marketing specialist at G2 in India. He is an engineer with a keen interest in data analytics and cybersecurity. He writes about topics related to them. You can find him reading books, learning a new language, or playing pool in his free time.
