Immagina questo: stai facendo shopping online per un laptop ad alte prestazioni.
Ne clicchi uno e compaiono diversi suggerimenti simili. Sono vicini a ciò che stai cercando ma non sono gli stessi. Come fa il sito web a sapere quali sono pertinenti alla tua ricerca?
È qui che entra in gioco la similarità coseno – uno strumento matematico che misura la similarità tra due vettori non nulli in uno spazio ad alta dimensione.
I database vettoriali nei motori di ricerca e nei sistemi di raccomandazione utilizzano la similarità coseno per capire quanto strettamente i prodotti o le query di ricerca in un database corrispondano in base alle loro rappresentazioni vettoriali. Comprendere queste relazioni e modelli tra gli elementi permette alle soluzioni di database vettoriali di recuperare suggerimenti personalizzati e precisi che ti mantengono a navigare – e magari anche a comprare.
Cos'è la similarità coseno?
La similarità coseno è una metrica matematica che misura la similarità tra due vettori in un prodotto interno o spazio multidimensionale. Utilizza il coseno dell'angolo tra due vettori per determinare se puntano nella stessa direzione, indipendentemente dalle loro magnitudini.
In altre parole, la similarità coseno è il prodotto scalare di due vettori diviso per il prodotto delle loro magnitudini. È anche conosciuta come similarità di Orchini e coefficiente di congruenza di Tucker.
Data scientists, ingegneri di machine learning e sviluppatori software utilizzano la similarità coseno per confrontare migliaia di punti dati e comprendere le loro relazioni senza perdersi nei dettagli. È ampiamente utilizzata per misurare la similarità in text mining, recupero informativo e applicazioni di analisi del testo.
Altre misure di similarità popolari includono la distanza euclidea, la distanza di Manhattan, la similarità di Jaccard e la distanza di Minkowski.
Perché la similarità coseno è importante?
La similarità coseno fornisce un modo robusto per valutare la similarità semantica tra documenti, dataset e immagini ad alta dimensione e sparsi. È efficace perché si concentra sull'orientamento di due vettori in uno spazio, misurando la loro similarità indipendentemente dalla loro magnitudine.
Le applicazioni di analisi del testo che utilizzano la frequenza dei termini-inverso della frequenza nei documenti (TF-IDF), Word2Vec e rappresentazioni di codificatori bidirezionali da trasformatori (BERT) derivano vettori di parole con grandi dimensioni ma bassa sovrapposizione. Le metriche di similarità tradizionali come la distanza euclidea sono sensibili alle lunghezze dei vettori e non possono gestire questi vettori. La similarità coseno può facilmente concentrarsi sulla correlazione dei dati in tali scenari.
La similarità coseno aiuta anche le applicazioni di recupero informativo a classificare i documenti in base a quanto bene corrispondono a una query, anche quando i documenti variano in lunghezza o complessità.
La scalabilità della similarità coseno nello spazio vettoriale ad alta dimensione la rende inestimabile per i database vettoriali, dove trovare i vicini più prossimi rapidamente e accuratamente è necessario per il recupero delle immagini, i sistemi di raccomandazione e il rilevamento delle anomalie.
Il natural language processing (NLP) si basa sulla similarità coseno per confrontare efficacemente gli embedding vettoriali. Questo confronto di embedding aiuta gli algoritmi di NLP a classificare, raggruppare o raccomandare contenuti basati sulla similarità semantica dei documenti.
Vuoi saperne di più su Software di database vettoriale? Esplora i prodotti Database vettoriale.
Come funziona la similarità coseno?
La similarità coseno quantifica la similarità tra due vettori calcolando il coseno dell'angolo tra di essi. Di seguito è riportata la suddivisione di come funziona la similarità coseno in ambienti di dati ad alta dimensione e sparsi.
- Rappresentazione vettoriale: Il primo passo consiste nel convertire oggetti come parole, documenti, immagini o testi in vettori in uno spazio ad alta dimensione. Ogni dimensione del vettore rappresenta un singolo oggetto, con il suo valore che mostra la frequenza del vettore o la sua importanza.
- Prodotto scalare: Il prodotto scalare quantifica la relazione tra due vettori moltiplicando i loro componenti corrispondenti e sommando i risultati. Calcolare questo prodotto scalare è fondamentale per comprendere l'allineamento tra vettori nella stessa direzione.
- Calcolo della magnitudine: Il passo successivo consiste nel calcolare le lunghezze o magnitudini di ciascun vettore.
- Similarità coseno: Il punteggio di similarità coseno è il prodotto scalare diviso per il prodotto delle magnitudini dei due vettori.
Dividere il prodotto scalare per il prodotto delle magnitudini dei vettori normalizza il risultato della similarità a un intervallo tra -1 e 1. Questa normalizzazione assicura che il punteggio di similarità rifletta solo l'angolo di orientamento dei vettori, non la loro magnitudine. Misura costantemente la similarità dei vettori, indipendentemente dalla scala dei dati.
Come calcolare la similarità coseno
Calcolare la similarità coseno richiede di trovare il prodotto scalare di due vettori. Poi, moltiplica le magnitudini di quei due vettori. Ora, dividi il prodotto scalare per il prodotto delle magnitudini per trovare il punteggio di similarità coseno.
Formula della similarità coseno
Il punteggio di similarità coseno tra due vettori, A e B, è calcolato usando la formula seguente:
Similarità Coseno (A, B) = (A·B) / (||A|| * ||B||)
Dove,
A · B è il prodotto scalare dei vettori A e B
||A|| e ||B|| rappresentano la lunghezza o magnitudine dei due vettori A e B
||A|| * ||B|| denota il prodotto delle magnitudini dei vettori A e B
La similarità coseno varia tra -1 e 1.
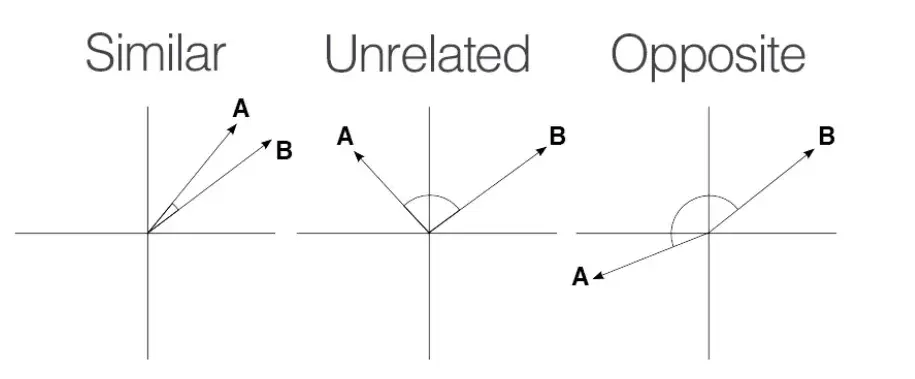Fonte: Medium
Un punteggio di 1 significa che i vettori sono perfettamente allineati o proporzionali, indicando la massima similarità.
Un punteggio di 0 implica che i vettori sono ortogonali, il che significa che non hanno similarità.
Un punteggio di -1 mostra che i vettori sono perfettamente opposti, il che significa che puntano in direzioni opposte ma hanno la stessa magnitudine.
Esempio di similarità coseno
Calcoliamo la similarità coseno tra i vettori A e B.
Il vettore A ha valori, A = { 1, 9, 3, 6 } Il vettore 'B' ha valori, B = { 1, 7, 0, 1 }
Prodotto scalare: A·B = 1×1 + 9×7 + 3×0 + 6×1 =70
Magnitudine di A: ||A|| = √(1² + 9² + 3² + 6²) = √(1 + 81 + 9 + 36) = √127 ≈ 11.27
Magnitudine di B: ||B|| = √(1² + 7² + 0² + 1²) = √(1 + 49 + 0 + 1) = √51 ≈ 7.14
Similarità Coseno = (A · B) / (||A|| * ||B||) = 70 / (11.27 × 7.14) ≈ 0.87
La similarità coseno tra i vettori A e B è approssimativamente 0.87, il che mostra una sostanziale similarità tra di essi.
Librerie per il calcolo della similarità coseno
Calcolare la similarità coseno è semplice ma può essere difficile quando si lavora con grandi dataset. In tali situazioni, puoi utilizzare linguaggi di programmazione come Python e librerie e strumenti come Matlab, SciKit-Learn, TensorFlow e SciPy.
NumPy
NumPy è una potente libreria Python per calcoli numerici. Supporta operazioni su array multidimensionali, matrici e funzioni matematiche, rendendola ideale per i calcoli di similarità coseno.
Come calcolare la similarità coseno usando NumPy
# importa le librerie richieste
import numpy as np
from numpy.linalg import norm
# definisci due liste o array
A = np.array([1, 9, 3, 6])
B = np.array([1, 7, 0, 1])
print("A:", A)
print("B:", B)
# calcola la similarità coseno
cosine = np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B))
print("Similarità Coseno:", cosine)
SciKit-Learn
SciKit-Learn è una libreria di machine learning basata su Python con funzioni integrate per compiti di analisi dei dati, inclusa la similarità coseno. Il modulo sklearn.metrics.pairwise offre una funzione cosine_similarity per gestire sia matrici dense che sparse.
Come calcolare la similarità coseno usando SciKit-Learn
# importa le librerie richieste
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
# definisci i vettori
A = np.array([[1, 9, 3, 6]])
B = np.array([[1, 7, 0, 1]])
# calcola la similarità coseno
cosine_sim = cosine_similarity(A, B)
print("Similarità Coseno:", cosine_sim[0][0])
SciPy
SciPy è un'altra popolare libreria basata su Python per il calcolo scientifico. Costruita su NumPy, SciPy presenta funzioni ottimizzate che calcolano la similarità coseno per grandi dataset. Il suo modulo scipy.spatial.distance include una funzione di calcolo della distanza coseno, che puoi usare per calcolare la similarità coseno.
Come calcolare la similarità coseno usando SciPy
# importa le librerie richieste
import numpy as np
from scipy.spatial.distance import cosine
# definisci i vettori
A = np.array([1, 9, 3, 6])
B = np.array([1, 7, 0, 1])
# calcola la distanza coseno
cosine_distance = cosine(A, B)
# calcola la similarità coseno
cosine_similarity = 1 - cosine_distance
print("Similarità Coseno:", cosine_similarity)
Gensim
Gensim è una libreria Python ampiamente utilizzata per il topic modeling e il natural language processing. Presenta funzioni integrate per calcolare la similarità coseno tra un grande volume di documenti di testo e vettori di parole.
Come calcolare la similarità coseno usando Gensim
# importa le librerie richieste
from gensim import corpora
from gensim.matutils import sparse2full
from gensim.similarities import MatrixSimilarity
from gensim.models import TfidfModel
import numpy as np
# documenti di esempio
documents = [
"I love playing football.",
"Football is a great sport.",
"I enjoy watching movies.",
"Movies are entertaining.",
]
# tokenizza e preelabora
texts = [[word.lower() for word in doc.split()] for doc in documents]
# crea un dizionario e un corpus
dictionary = corpora.Dictionary(texts)
corpus = [dictionary.doc2bow(text) for text in texts]
# crea un modello TF-IDF
tfidf_model = TfidfModel(corpus)
tfidf_corpus = tfidf_model[corpus]
# crea un indice di similarità
index = MatrixSimilarity(tfidf_corpus)
# calcola la similarità del primo documento con tutti gli altri
similarities = index[tfidf_corpus[0]]
# stampa le similarità
print("Similarità Coseno per il Documento 0:", similarities)
TensorFlow e PyTorch
TensorFlow e PyTorch sono popolari librerie di deep learning che aiutano a misurare la similarità tra vettori di caratteristiche ad alta dimensione.
Come calcolare la similarità coseno usando TensorFlow
# importa le librerie richieste
import tensorflow as tf
# definisci i vettori
A = tf.constant([1.0, 9.0, 3.0, 6.0])
B = tf.constant([1.0, 7.0, 0.0, 1.0])
# calcola la similarità coseno
def cosine_similarity(A, B):
# calcola il prodotto scalare
dot_product = tf.reduce_sum(A * B)
# calcola la norma (magnitudine) dei vettori
norm_A = tf.sqrt(tf.reduce_sum(tf.square(A)))
norm_B = tf.sqrt(tf.reduce_sum(tf.square(B)))
# calcola la similarità coseno
cosine_sim = dot_product / (norm_A * norm_B)
return cosine_sim
similarity = cosine_similarity(A, B)
print("Similarità Coseno:", similarity.numpy())
# calcola la similarità coseno
cosine_similarity = 1 - cosine_distance
print("Similarità Coseno:", cosine_similarity)
Quando si utilizza PyTorch, gli sviluppatori possono usare torch.tensor() per creare oggetti tensor e usare la funzione torch.norm() per calcolare la norma euclidea dei vettori.
Considera di usare i suggerimenti seguenti per ottimizzare i calcoli coseno in Python:
- Opta per librerie ottimizzate. Usa le operazioni vettorializzate di NumPy o SciKit-Learn per calcolare la similarità coseno e ridurre il sovraccarico dei cicli Python. Queste librerie eseguono anche più velocemente rispetto al Python di base.
- Usa Numba. Numba è un compilatore just-in-time (JIT) open-source per codice Python e NumPy. Ti aiuta a parallelizzare automaticamente i calcoli di similarità coseno usando più unità di elaborazione centrale (CPU).
- Impiega matrici sparse. Considera di usare le rappresentazioni di matrici sparse di SciPy quando gestisci dataset con molti valori zero. Ti aiuterà a risparmiare memoria e tempo di calcolo per compiti di analisi della similarità di testo e documenti.
- Usa Cython per la compilazione del codice. Cython permette agli sviluppatori di scrivere codici simili a C con una sintassi simile a Python. Usarlo per la compilazione del codice li aiuta a raggiungere velocità simili a C o C++ mantenendo la facilità della sintassi Python.
- Usa algoritmi ANN. Gli algoritmi di vicini approssimati più prossimi o ANN come KD-Tress o hashing sensibile alla località (LSH) aiutano a trovare vettori simili senza calcolare la similarità coseno. Questi algoritmi possono essere utili per applicazioni su larga scala.
- Accedi alle GPU. Usare unità di elaborazione grafica o GPU con librerie Python come TensorFlow può anche aiutare a raggiungere una maggiore produttività quando si lavora con dataset estesi ad alta dimensione.
Similarità coseno vs. altri metodi per il calcolo della similarità
La similarità coseno non è l'unico metodo per misurare la similarità tra oggetti in un set di dati. Altri metodi di calcolo della similarità popolari sono:
Distanza euclidea
La distanza euclidea misura la distanza in linea retta tra due punti nello spazio euclideo. È sempre zero o positiva. Potresti non essere in grado di trovare una distanza euclidea significativa in spazi ad alta dimensione poiché i punti tendono a convergere.
La similarità coseno è ideale per dati ad alta dimensione o analisi del testo dove la magnitudine del vettore non è essenziale. La similarità euclidea funziona meglio per spazi a bassa dimensione dove la magnitudine del vettore è vitale.
Distanza di Manhattan
Questa misura la distanza tra due punti in un percorso a griglia sommando le differenze assolute tra le loro coordinate. A differenza della distanza euclidea, la distanza di Manhattan è meno sensibile ai valori anomali, motivo per cui è adatta per compiti di clustering.
Usa la distanza di Manhattan per considerare le differenze assolute tra le coordinate ma la similarità coseno quando la direzione dei vettori è più importante della magnitudine.
Distanza di Hamming
La distanza di Hamming confronta due stringhe di dati binari di uguale lunghezza quantificando il numero di posizioni di bit tra due bit. Misura il numero di posizioni in cui i simboli corrispondenti di due stringhe differiscono.
La distanza di Hamming è sempre un intero non negativo poiché la distanza è il conteggio totale di queste discrepanze. I compiti di classificazione nel machine learning e gli algoritmi di rilevamento degli errori usano la distanza di Hamming per confrontare vettori binari.
Similarità di Jaccard
La similarità di Jaccard, conosciuta anche come coefficiente di Jaccard o indice di Jaccard, è un'altra misura di prossimità che calcola la similarità tra due vettori o oggetti binari asimmetrici. Puoi calcolarla dividendo la dimensione dell'intersezione degli insiemi per la dimensione dell'unione degli insiemi.
La similarità di Jaccard è migliore per confrontare la presenza o assenza di termini, mentre la similarità coseno eccelle nel misurare l'angolo tra vettori in dati densi con termini sovrapposti.
Vantaggi della similarità coseno
Il principale vantaggio è che la similarità coseno cattura l'aspetto direzionale dei dati senza essere influenzata dai cambiamenti di magnitudine del vettore. Le applicazioni di analisi del testo, i sistemi di raccomandazione e le soluzioni NLP usano la similarità coseno per facilitare il calcolo e ridurre efficacemente le dimensioni del vettore.
- Invarianza di magnitudine: La similarità coseno misura la direzione di due vettori e non distorce il punteggio di prossimità anche quando differiscono in lunghezza. La sua natura invariante alla scala la rende ideale per motori di ricerca e applicazioni basate su testo, dove si concentra sul fatto che i vettori coprano argomenti simili invece che sulla lunghezza, il conteggio delle parole o la verbosità.
- Scalabilità per dati sparsi: La similarità coseno utilizza la rilevanza direzionale per comprimere efficacemente i dati con grandi dimensioni. Il risultato è un tempo di calcolo rapido per dataset sparsi e ad alta dimensione, rendendo la similarità coseno ideale per database vettoriali e sistemi di recupero delle immagini.
- Riduzione della dimensionalità: La similarità coseno è compatibile con tecniche come l'analisi delle componenti principali (PCA) e l'incorporamento stocastico distribuito t-distributed (t-SNE). Questi metodi riducono il numero di dimensioni preservando la varianza in un dataset. L'attenzione della similarità coseno alle relazioni angolari assicura che i punti dati rimangano robusti anche dopo che queste trasformazioni mappano i vettori in uno spazio a dimensione inferiore.
- Similarità semantica: Il punteggio di similarità coseno utilizza modelli di spazio vettoriale per confrontare le parole in base ai loro significati invece che ai conteggi di parole grezze o alle similarità sintattiche. I migliori motori di ricerca di database vettoriali si affidano a questa capacità per misurare la distanza tra parole o frasi vettorializzate in analisi del sentimento, modellazione degli argomenti e compiti di traduzione automatica.
Svantaggi della similarità coseno
Nonostante i suoi numerosi vantaggi, la similarità coseno soffre di svantaggi, tra cui:
- Maledizione della dimensionalità: La similarità coseno può affrontare sfide nell'analisi dei dati in spazi ad alta dimensione, un fenomeno popolarmente noto come la maledizione della dimensionalità. Le distanze aumentate tra i punti dati causano la convergenza degli angoli tra i vettori, rendendo difficile differenziarli usando la similarità coseno.
- Sensibilità ai dati sparsi: La similarità coseno fatica anche a fornire intuizioni significative in dataset sparsi con molte voci zero nei vettori.
- Non considera la differenza assoluta: Poiché la similarità coseno si concentra su un angolo invece che sulla magnitudine dei vettori, può trascurare le differenze di magnitudine, che possono trasmettere informazioni contestuali cruciali.
- Alta dipendenza dalla rappresentazione vettoriale: La similarità coseno può restituire risultati inaccurati per rappresentazioni vettoriali di documenti mal costruite.
Applicazioni della similarità coseno
La similarità coseno è utilizzata nel recupero informativo, nel text mining, nei sistemi di raccomandazione, nell'elaborazione delle immagini, nella classificazione dei documenti e nel clustering.
“Usiamo la similarità coseno per misurare la similarità tra il testo originale e il testo generato dall'IA. Ci aiuta a migliorare l'originalità del testo generato dall'IA e a personalizzarlo per la soddisfazione e il coinvolgimento dell'utente.”
Robert Brown
Co-fondatore di AI Humanize
Recupero informativo
I sistemi di recupero informativo come i motori di ricerca usano la similarità coseno per trovare documenti pertinenti nel database per le query di ricerca. Questa ricerca di similarità assicura che gli utenti ottengano documenti di valore. In questi casi, l'incorporamento del testo si basa su modelli complessi di reti neurali come Word2Vec, GloVe o LLM come GPT, BERT e LLaMa.
Sistemi di raccomandazione
Piattaforme di streaming di film come Netflix si affidano alla similarità coseno per condividere raccomandazioni basate sulla cronologia di visione degli utenti. Questi sistemi considerano ogni film e utente come vettori. Dopo aver generato l'incorporamento vettoriale usando la fattorizzazione della matrice o gli autoencoder, usano la similarità coseno per raccomandare film basati sulle preferenze degli utenti e sui modelli di visione passati.
Elaborazione delle immagini
I sistemi di riconoscimento facciale, le applicazioni di imaging medico e i veicoli a guida autonoma si affidano ai punteggi di similarità coseno per valutare la similarità tra le immagini. Usano reti neurali convoluzionali per generare incorporamenti per le immagini e catturare modelli visivi tra di esse.
Suggerimenti per l'uso della similarità coseno:
- Preelabora i dati: Considera di rimuovere le parole comuni di stop con poco o nessun valore semantico – inoltre, usa lo stemming o la lemmatizzazione per ridurre le parole alla loro forma base e standardizzare il dataset.
- Usa il ponderamento dei termini: Impiega la tecnica TF-IDF per assegnare pesi alle parole rare che appaiono frequentemente nei documenti. Questo ponderamento aiuta nella differenziazione efficiente dei vettori.
- Opta per una dimensione del dataset più grande: Usare dataset più grandi ti permette di esplorare una gamma più ampia di argomenti e stili, rendendo più facile confrontare le similarità.
Angola il tuo gioco di dati
Il focus della similarità coseno sugli angoli invece che sulla magnitudine la rende ideale per la raccomandazione di contenuti, l'analisi del testo, il clustering dei documenti e il data mining. È indubbiamente la scelta migliore per confrontare gli embedding dei trasformatori grazie alla sua natura invariante alla scala e alla capacità di gestire dati ad alta dimensione. Considera il problema e i requisiti dei dati per trovare il metodo di calcolo della similarità più appropriato.
Cerchi software con architettura event-driven per l'elaborazione dei dati in tempo reale? Dai un'occhiata alle migliori soluzioni di database analitico in tempo reale.
Sagar Joshi
Sagar Joshi is a former content marketing specialist at G2 in India. He is an engineer with a keen interest in data analytics and cybersecurity. He writes about topics related to them. You can find him reading books, learning a new language, or playing pool in his free time.
