Stellen Sie sich vor: Sie kaufen online einen leistungsstarken Laptop.
Sie klicken auf einen, und mehrere ähnliche Vorschläge erscheinen. Sie sind nah an dem, was Sie suchen, aber nicht dasselbe. Woher weiß die Website, welche relevant für Ihre Suche sind?
Hier kommt die Kosinus-Ähnlichkeit ins Spiel – ein mathematisches Werkzeug, das die Ähnlichkeit zwischen zwei nicht-null Vektoren in einem hochdimensionalen Raum misst.
Vektordatenbanken in Suchmaschinen und Empfehlungssystemen verwenden die Kosinus-Ähnlichkeit, um zu verstehen, wie eng Produkte oder Suchanfragen in einer Datenbank basierend auf ihren Vektordarstellungen übereinstimmen. Das Verständnis dieser Beziehungen und Muster zwischen den Elementen ermöglicht es Vektordatenbanklösungen, personalisierte, punktgenaue Vorschläge abzurufen, die Sie zum Stöbern – und vielleicht sogar zum Kaufen – anregen.
Was ist Kosinus-Ähnlichkeit?
Kosinus-Ähnlichkeit ist eine mathematische Metrik, die die Ähnlichkeit zwischen zwei Vektoren in einem inneren Produkt oder mehrdimensionalen Raum misst. Sie verwendet den Kosinus des Winkels zwischen zwei Vektoren, um zu bestimmen, ob sie in die gleiche Richtung zeigen, unabhängig von ihren Größen.
Mit anderen Worten, die Kosinus-Ähnlichkeit ist das Skalarprodukt zweier Vektoren, geteilt durch das Produkt ihrer Größen. Sie ist auch als Orchini-Ähnlichkeit und Tucker-Kongruenzkoeffizient bekannt.
Datenwissenschaftler, Ingenieure für maschinelles Lernen und Softwareentwickler verwenden die Kosinus-Ähnlichkeit, um Tausende von Datenpunkten zu vergleichen und ihre Beziehungen zu verstehen, ohne sich in den Details zu verlieren. Sie wird häufig zur Messung der Ähnlichkeit in Text-Mining, Informationsabruf und Textanalyse-Anwendungen verwendet.
Andere beliebte Ähnlichkeitsmaße sind euklidische Distanz, Manhattan-Distanz, Jaccard-Ähnlichkeit und Minkowski-Distanz.
Warum ist Kosinus-Ähnlichkeit wichtig?
Kosinus-Ähnlichkeit bietet eine robuste Möglichkeit, die semantische Ähnlichkeit zwischen hochdimensionalen, spärlichen Dokumenten, Datensätzen und Bildern zu bewerten. Sie ist effektiv, weil sie sich auf die Ausrichtung zweier Vektoren in einem Raum konzentriert und ihre Ähnlichkeit unabhängig von ihrer Größe misst.
Textanalyse-Anwendungen, die Termfrequenz-Inverse-Dokumentfrequenz (TF-IDF), Word2Vec und bidirektionale Encoder-Darstellungen von Transformatoren (BERT) Methoden verwenden, leiten Wortvektoren mit großen Dimensionen, aber geringer Überlappung ab. Traditionelle Ähnlichkeitsmetriken wie die euklidische Distanz sind empfindlich gegenüber Vektorlängen und können diese Vektoren nicht handhaben. Kosinus-Ähnlichkeit kann sich in solchen Szenarien leicht auf die Datenkorrelation konzentrieren.
Die Kosinus-Ähnlichkeit hilft auch Informationsabrufanwendungen, Dokumente basierend darauf zu bewerten, wie gut sie zu einer Abfrage passen, selbst wenn die Dokumente in Länge oder Komplexität variieren.
Die Skalierbarkeit der Kosinus-Ähnlichkeit im hochdimensionalen Vektorraum macht sie für Vektordatenbanken unverzichtbar, wo das schnelle und genaue Finden nächster Nachbarn für die Bildsuche, Empfehlungssysteme und Anomalieerkennung notwendig ist.
Die Verarbeitung natürlicher Sprache (NLP) verlässt sich auf die Kosinus-Ähnlichkeit, um Vektoreinbettungen effizient zu vergleichen. Dieser Einbettungsvergleich unterstützt NLP-Algorithmen bei der Klassifizierung, Clusterbildung oder Empfehlung von Inhalten basierend auf der semantischen Ähnlichkeit von Dokumenten.
Möchten Sie mehr über Vektordatenbank-Software erfahren? Erkunden Sie Vektordatenbank Produkte.
Wie funktioniert die Kosinus-Ähnlichkeit?
Die Kosinus-Ähnlichkeit quantifiziert die Ähnlichkeit zwischen zwei Vektoren, indem sie den Kosinus des Winkels zwischen ihnen berechnet. Nachfolgend ist die Aufschlüsselung, wie die Kosinus-Ähnlichkeit in hochdimensionalen, spärlichen Datenumgebungen funktioniert.
- Vektordarstellung: Der erste Schritt besteht darin, Objekte wie Wörter, Dokumente, Bilder oder Texte in Vektoren in einem hochdimensionalen Raum zu konvertieren. Jede Vektordimension repräsentiert ein einzelnes Objekt, wobei ihr Wert die Vektorhäufigkeit oder ihre Bedeutung zeigt.
- Skalarprodukt: Das Skalarprodukt quantifiziert die Beziehung zwischen zwei Vektoren, indem es ihre entsprechenden Komponenten multipliziert und die Ergebnisse summiert. Die Berechnung dieses Skalarprodukts ist entscheidend, um die Ausrichtung zwischen Vektoren in die gleiche Richtung zu verstehen.
- Berechnung der Größe: Der nächste Schritt besteht darin, die Längen oder Größen jedes Vektors zu berechnen.
- Kosinus-Ähnlichkeit: Der Kosinus-Ähnlichkeitswert ist das Skalarprodukt geteilt durch das Produkt der Größen der beiden Vektoren.
Das Teilen des Skalarprodukts durch das Produkt der Vektoren-Größen normalisiert das Ähnlichkeitsergebnis auf einen Bereich zwischen -1 und 1. Diese Normalisierung stellt sicher, dass der Ähnlichkeitswert nur den Orientierungswinkel der Vektoren widerspiegelt, nicht ihre Größe. Es misst konsistent die Ähnlichkeit von Vektoren, unabhängig von der Skalierung der Daten.
Wie berechnet man die Kosinus-Ähnlichkeit
Die Berechnung der Kosinus-Ähnlichkeit erfordert das Finden des Skalarprodukts zweier Vektoren. Dann multiplizieren Sie die Größen dieser beiden Vektoren. Teilen Sie nun das Skalarprodukt durch das Produkt der Größen, um den Kosinus-Ähnlichkeitswert zu finden.
Kosinus-Ähnlichkeitsformel
Der Kosinus-Ähnlichkeitswert zwischen zwei Vektoren, A und B, wird mit der untenstehenden Formel berechnet:
Kosinus-Ähnlichkeit (A, B) = (A·B) / (||A|| * ||B||)
Wo,
A · B ist das Skalarprodukt der Vektoren A und B
||A|| und ||B|| repräsentieren die Länge oder Größe der beiden Vektoren A und B
||A|| * ||B|| bezeichnet das Produkt der Größen der Vektoren A und B
Die Kosinus-Ähnlichkeit reicht von -1 bis 1.
 Quelle: Medium
Quelle: Medium
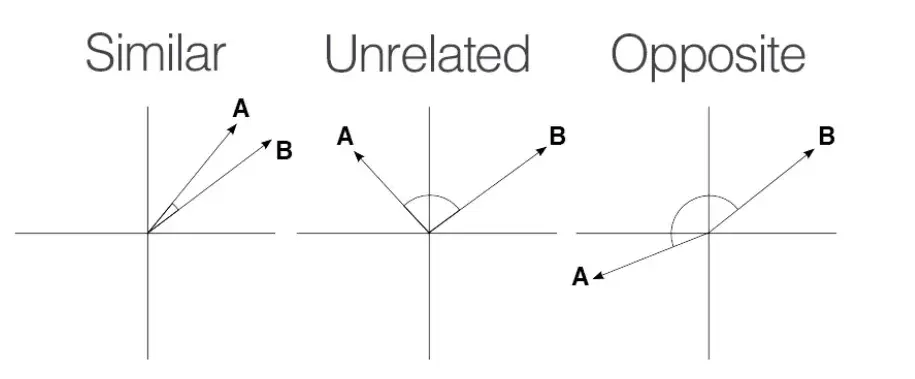
Ein Wert von 1 bedeutet, dass die Vektoren perfekt ausgerichtet oder proportional sind, was maximale Ähnlichkeit anzeigt.
Ein Wert von 0 impliziert, dass die Vektoren orthogonal sind, was bedeutet, dass sie keine Ähnlichkeit haben.
Ein Wert von -1 zeigt, dass die Vektoren perfekt entgegengesetzt sind, was bedeutet, dass sie in entgegengesetzte Richtungen zeigen, aber die gleiche Größe haben.
Beispiel für Kosinus-Ähnlichkeit
Lassen Sie uns die Kosinus-Ähnlichkeit zwischen den Vektoren A und B berechnen.
Der A-Vektor hat die Werte, A = { 1, 9, 3, 6 } Der 'B'-Vektor hat die Werte, B = { 1, 7, 0, 1 }
Skalarprodukt: A·B = 1×1 + 9×7 + 3×0 + 6×1 =70
Größe von A: ||A|| = √(1² + 9² + 3² + 6²) = √(1 + 81 + 9 + 36) = √127 ≈ 11.27
Größe von B: ||B|| = √(1² + 7² + 0² + 1²) = √(1 + 49 + 0 + 1) = √51 ≈ 7.14
Kosinus-Ähnlichkeit = (A · B) / (||A|| * ||B||) = 70 / (11.27 × 7.14) ≈ 0.87
Die Kosinus-Ähnlichkeit zwischen den Vektoren A und B beträgt ungefähr 0.87, was eine erhebliche Ähnlichkeit zwischen ihnen zeigt.
Bibliotheken zur Berechnung der Kosinus-Ähnlichkeit
Die Berechnung der Kosinus-Ähnlichkeit ist einfach, kann jedoch schwierig sein, wenn mit großen Datensätzen gearbeitet wird. In solchen Situationen können Sie Programmiersprachen wie Python und Bibliotheken und Tools wie Matlab, SciKit-Learn, TensorFlow und SciPy verwenden.
NumPy
NumPy ist eine leistungsstarke Python-Bibliothek für numerische Berechnungen. Sie unterstützt mehrdimensionale Array-Operationen, Matrizen und mathematische Funktionen, was sie ideal für Kosinus-Ähnlichkeitsberechnungen macht.
Wie man die Kosinus-Ähnlichkeit mit NumPy berechnet
# erforderliche Bibliotheken importieren
import numpy as np
from numpy.linalg import norm
# zwei Listen oder Arrays definieren
A = np.array([1, 9, 3, 6])
B = np.array([1, 7, 0, 1])
print("A:", A)
print("B:", B)
# Kosinus-Ähnlichkeit berechnen
cosine = np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B))
print("Kosinus-Ähnlichkeit:", cosine)
SciKit-Learn
SciKit-Learn ist eine Python-basierte maschinelle Lernbibliothek mit integrierten Funktionen für Datenanalysetasks, einschließlich Kosinus-Ähnlichkeit. Das Modul sklearn.metrics.pairwise bietet eine cosine_similarity-Funktion, die sowohl dichte als auch spärliche Matrizen handhaben kann.
Wie man die Kosinus-Ähnlichkeit mit SciKit-Learn berechnet
# erforderliche Bibliotheken importieren
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
# die Vektoren definieren
A = np.array([[1, 9, 3, 6]])
B = np.array([[1, 7, 0, 1]])
# Kosinus-Ähnlichkeit berechnen
cosine_sim = cosine_similarity(A, B)
print("Kosinus-Ähnlichkeit:", cosine_sim[0][0])
SciPy
SciPy ist eine weitere beliebte Python-basierte Bibliothek für wissenschaftliches Rechnen. Auf NumPy aufgebaut, bietet SciPy optimierte Funktionen, die die Kosinus-Ähnlichkeit für große Datensätze berechnen. Das Modul scipy.spatial.distance enthält eine Funktion zur Berechnung der Kosinus-Distanz, die Sie zur Berechnung der Kosinus-Ähnlichkeit verwenden können.
Wie man die Kosinus-Ähnlichkeit mit SciPy berechnet
# erforderliche Bibliotheken importieren
import numpy as np
from scipy.spatial.distance import cosine
# die Vektoren definieren
A = np.array([1, 9, 3, 6])
B = np.array([1, 7, 0, 1])
# Kosinus-Distanz berechnen
cosine_distance = cosine(A, B)
# Kosinus-Ähnlichkeit berechnen
cosine_similarity = 1 - cosine_distance
print("Kosinus-Ähnlichkeit:", cosine_similarity)
Gensim
Gensim ist eine Python-Bibliothek, die häufig für Themenmodellierung und Verarbeitung natürlicher Sprache verwendet wird. Sie bietet integrierte Funktionen zur Berechnung der Kosinus-Ähnlichkeit zwischen einer großen Menge von Textdokumenten und Wortvektoren.
Wie man die Kosinus-Ähnlichkeit mit Gensim berechnet
# erforderliche Bibliotheken importieren
from gensim import corpora
from gensim.matutils import sparse2full
from gensim.similarities import MatrixSimilarity
from gensim.models import TfidfModel
import numpy as np
# Beispieldokumente
documents = [
"I love playing football.",
"Football is a great sport.",
"I enjoy watching movies.",
"Movies are entertaining.",
]
# tokenisieren und vorverarbeiten
texts = [[word.lower() for word in doc.split()] for doc in documents]
# ein Wörterbuch und Korpus erstellen
dictionary = corpora.Dictionary(texts)
corpus = [dictionary.doc2bow(text) for text in texts]
# ein TF-IDF-Modell erstellen
tfidf_model = TfidfModel(corpus)
tfidf_corpus = tfidf_model[corpus]
# einen Ähnlichkeitsindex erstellen
index = MatrixSimilarity(tfidf_corpus)
# die Ähnlichkeit des ersten Dokuments mit allen anderen berechnen
similarities = index[tfidf_corpus[0]]
# die Ähnlichkeiten ausgeben
print("Kosinus-Ähnlichkeiten für Dokument 0:", similarities)
TensorFlow und PyTorch
TensorFlow und PyTorch sind beliebte Deep-Learning-Bibliotheken, die helfen, die Ähnlichkeit zwischen hochdimensionalen Merkmalsvektoren zu messen.
Wie man die Kosinus-Ähnlichkeit mit TensorFlow berechnet
# erforderliche Bibliotheken importieren
import tensorflow as tf
# die Vektoren definieren
A = tf.constant([1.0, 9.0, 3.0, 6.0])
B = tf.constant([1.0, 7.0, 0.0, 1.0])
# Kosinus-Ähnlichkeit berechnen
def cosine_similarity(A, B):
# das Skalarprodukt berechnen
dot_product = tf.reduce_sum(A * B)
# die Norm (Größe) der Vektoren berechnen
norm_A = tf.sqrt(tf.reduce_sum(tf.square(A)))
norm_B = tf.sqrt(tf.reduce_sum(tf.square(B)))
# Kosinus-Ähnlichkeit berechnen
cosine_sim = dot_product / (norm_A * norm_B)
return cosine_sim
similarity = cosine_similarity(A, B)
print("Kosinus-Ähnlichkeit:", similarity.numpy())
# Kosinus-Ähnlichkeit berechnen
cosine_similarity = 1 - cosine_distance
print("Kosinus-Ähnlichkeit:", cosine_similarity)
Bei der Verwendung von PyTorch können Entwickler torch.tensor() verwenden, um Tensor-Objekte zu erstellen, und die Funktion torch.norm() verwenden, um die euklidische Norm der Vektoren zu berechnen.
Berücksichtigen Sie die folgenden Tipps, um Kosinus-Berechnungen in Python zu optimieren:
- Optimierte Bibliotheken verwenden. Verwenden Sie die vektorisierten Operationen von NumPy oder SciKit-Learn, um die Kosinus-Ähnlichkeit zu berechnen und den Overhead von Python-Schleifen zu reduzieren. Diese Bibliotheken sind auch schneller als grundlegendes Python.
- Numba verwenden. Numba ist ein Open-Source-Just-in-Time (JIT) Compiler für Python- und NumPy-Code. Es hilft Ihnen, die Kosinus-Ähnlichkeitsberechnungen automatisch mit mehreren zentralen Verarbeitungseinheiten (CPUs) zu parallelisieren.
- Sparse-Matrizen verwenden. Erwägen Sie die Verwendung von SciPys spärlichen Matrixdarstellungen, wenn Sie mit Datensätzen mit vielen Nullwerten arbeiten. Es hilft Ihnen, Speicher und Rechenzeit für Aufgaben zur Text- und Dokumentähnlichkeitsanalyse zu sparen.
- Cython für die Code-Kompilierung verwenden. Cython ermöglicht es Entwicklern, C-ähnlichen Code mit einer Python-ähnlichen Syntax zu schreiben. Die Verwendung für die Code-Kompilierung hilft ihnen, Geschwindigkeiten ähnlich wie C oder C++ zu erreichen, während die Einfachheit der Python-Syntax beibehalten wird.
- ANN-Algorithmen verwenden. Ungefähre nächste Nachbarn oder ANN-Algorithmen wie KD-Trees oder lokalitätssensitives Hashing (LSH) helfen, ähnliche Vektoren zu finden, ohne die Kosinus-Ähnlichkeit zu berechnen. Diese Algorithmen können für groß angelegte Anwendungen nützlich sein.
- GPUs verwenden. Die Verwendung von grafischen Verarbeitungseinheiten oder GPUs mit Python-Bibliotheken wie TensorFlow kann auch helfen, einen höheren Durchsatz zu erreichen, wenn mit umfangreichen hochdimensionalen Datensätzen gearbeitet wird.
Kosinus-Ähnlichkeit vs. andere Methoden zur Ähnlichkeitsberechnung
Die Kosinus-Ähnlichkeit ist nicht die einzige Methode zur Messung der Ähnlichkeit zwischen Objekten in einem Datensatz. Andere beliebte Methoden zur Ähnlichkeitsberechnung sind:
Euklidische Distanz
Die euklidische Distanz misst die direkte Entfernung zwischen zwei Punkten im euklidischen Raum. Sie ist immer entweder null oder positiv. Sie können möglicherweise keine sinnvolle euklidische Distanz in hochdimensionalen Räumen finden, da Punkte dazu neigen, zu konvergieren.
Kosinus-Ähnlichkeit ist ideal für hochdimensionale Daten oder Textanalysen, bei denen die Vektormagnitude nicht entscheidend ist. Euklidische Ähnlichkeit funktioniert am besten für niedrigdimensionale Räume, in denen die Vektormagnitude wichtig ist.
Manhattan-Distanz
Diese misst die Entfernung zwischen zwei Punkten in einem rasterartigen Pfad, indem die absoluten Unterschiede zwischen ihren Koordinaten summiert werden. Im Gegensatz zur euklidischen Distanz ist die Manhattan-Distanz weniger empfindlich gegenüber Ausreißern, weshalb sie sich für Clustering-Aufgaben eignet.
Verwenden Sie die Manhattan-Distanz, um absolute Unterschiede zwischen Koordinaten zu berücksichtigen, aber die Kosinus-Ähnlichkeit, wenn die Richtung der Vektoren wichtiger ist als die Magnitude.
Hamming-Distanz
Die Hamming-Distanz vergleicht zwei binäre Datenstrings gleicher Länge, indem sie die Anzahl der Bitpositionen zwischen zwei Bits quantifiziert. Sie misst die Anzahl der Positionen, an denen sich die entsprechenden Symbole zweier Strings unterscheiden.
Die Hamming-Distanz ist immer eine nicht-negative ganze Zahl, da die Distanz die Gesamtanzahl dieser Unterschiede ist. Klassifikationsaufgaben im maschinellen Lernen und Fehlererkennungsalgorithmen verwenden die Hamming-Distanz, um binäre Vektoren zu vergleichen.
Jaccard-Ähnlichkeit
Die Jaccard-Ähnlichkeit, auch bekannt als Jaccard-Koeffizient oder Jaccard-Index, ist eine weitere Proximitätsmessung, die die Ähnlichkeit zwischen zwei asymmetrischen binären Vektoren oder Objekten berechnet. Sie können sie berechnen, indem Sie die Größe der Schnittmenge der Mengen durch die Größe der Vereinigung der Mengen teilen.
Die Jaccard-Ähnlichkeit eignet sich am besten zum Vergleich der Anwesenheit oder Abwesenheit von Begriffen, während die Kosinus-Ähnlichkeit beim Messen des Winkels zwischen Vektoren in dichten Daten mit überlappenden Begriffen hervorragend ist.
Vorteile der Kosinus-Ähnlichkeit
Der Hauptvorteil besteht darin, dass die Kosinus-Ähnlichkeit den Richtungsaspekt der Daten erfasst, ohne von Änderungen der Vektormagnitude beeinflusst zu werden. Textanalyse-Anwendungen, Empfehlungssysteme und NLP-Lösungen verwenden die Kosinus-Ähnlichkeit, um die Berechnung zu erleichtern und die Vektordimensionen effizient zu reduzieren.
- Größeninvarianz: Die Kosinus-Ähnlichkeit misst die Richtung zweier Vektoren und verzerrt den Proximitätswert nicht, selbst wenn sie sich in der Länge unterscheiden. Ihre skaleninvariante Natur macht sie ideal für Suchmaschinen und textbasierte Anwendungen, bei denen sie sich darauf konzentriert, ob Vektoren ähnliche Themen abdecken, anstatt auf die Länge, Wortanzahl oder Wortfülle.
- Skalierbarkeit für spärliche Daten: Die Kosinus-Ähnlichkeit verwendet die Richtungsrelevanz, um Daten mit großen Dimensionen effizient zu komprimieren. Das Ergebnis ist eine schnelle Berechnungszeit für spärliche, hochdimensionale Datensätze, was die Kosinus-Ähnlichkeit ideal für Vektordatenbanken und Bildabrufsysteme macht.
- Dimensionsreduktion: Die Kosinus-Ähnlichkeit ist kompatibel mit Techniken wie der Hauptkomponentenanalyse (PCA) und der t-verteilten stochastischen Nachbareinbettung (t-SNE). Diese Methoden reduzieren die Anzahl der Dimensionen, während die Varianz in einem Datensatz erhalten bleibt. Die Aufmerksamkeit der Kosinus-Ähnlichkeit auf Winkelbeziehungen stellt sicher, dass Datenpunkte robust bleiben, selbst nachdem diese Transformationen Vektoren in einen niedrigdimensionalen Raum abbilden.
- Semantische Ähnlichkeit: Der Kosinus-Ähnlichkeitswert verwendet Vektorraum-Modelle, um Wörter basierend auf ihren Bedeutungen zu vergleichen, anstatt auf rohen Wortanzahlen oder syntaktischen Ähnlichkeiten. Top-Vektordatenbank-Suchmaschinen verlassen sich auf diese Fähigkeit, um die Entfernung zwischen vektorisierten Wörtern oder Sätzen in Sentimentanalyse, Themenmodellierung und maschinellen Übersetzungsaufgaben zu messen.
Nachteile der Kosinus-Ähnlichkeit
Trotz ihrer vielen Vorteile leidet die Kosinus-Ähnlichkeit unter Nachteilen, einschließlich:
- Fluch der Dimensionalität: Die Kosinus-Ähnlichkeit kann Herausforderungen bei der Datenanalyse in hochdimensionalen Räumen gegenüberstehen, ein Phänomen, das als Fluch der Dimensionalität bekannt ist. Erhöhte Abstände zwischen Datenpunkten führen dazu, dass die Winkel zwischen Vektoren konvergieren, was es schwierig macht, sie mit der Kosinus-Ähnlichkeit zu unterscheiden.
- Empfindlichkeit gegenüber spärlichen Daten: Die Kosinus-Ähnlichkeit hat auch Schwierigkeiten, in spärlichen Datensätzen mit vielen Nullwerten in den Vektoren sinnvolle Einblicke zu bieten.
- Berücksichtigt keine absoluten Unterschiede: Da sich die Kosinus-Ähnlichkeit auf einen Winkel anstatt auf die Magnitude der Vektoren konzentriert, kann sie Magnitudenunterschiede übersehen, die entscheidende kontextuelle Informationen vermitteln können.
- Hohe Abhängigkeit von der Vektordarstellung: Die Kosinus-Ähnlichkeit kann ungenaue Ergebnisse für schlecht konstruierte Vektordarstellungen von Dokumenten liefern.
Anwendungen der Kosinus-Ähnlichkeit
Die Kosinus-Ähnlichkeit wird im Informationsabruf, Text-Mining, Empfehlungssystemen, Bildverarbeitung, Dokumentklassifizierung und Clustering verwendet.
„Wir verwenden die Kosinus-Ähnlichkeit, um die Ähnlichkeit zwischen dem Originaltext und dem KI-generierten Text zu messen. Sie hilft uns, die Originalität des KI-generierten Textes zu verbessern und ihn für Benutzerzufriedenheit und Engagement zu personalisieren.“
Robert Brown
Mitbegründer von AI Humanize
Informationsabruf
Informationsabrufsysteme wie Suchmaschinen verwenden die Kosinus-Ähnlichkeit, um relevante Dokumente in der Datenbank für Suchanfragen zu finden. Diese Ähnlichkeitssuche stellt sicher, dass Benutzer wertvolle Dokumente erhalten. In diesen Fällen verlässt sich die Texteingliederung auf komplexe neuronale Netzwerk-Modelle wie Word2Vec, GloVe oder LLMs wie GPT, BERT und LLaMa.
Empfehlungssysteme
Film-Streaming-Plattformen wie Netflix verlassen sich auf die Kosinus-Ähnlichkeit, um Empfehlungen basierend auf dem Sehverlauf der Benutzer zu teilen. Diese Systeme betrachten jeden Film und Benutzer als Vektoren. Nach der Generierung von Vektoreinbettungen mit Matrixfaktorisierung oder Autoencodern verwenden sie die Kosinus-Ähnlichkeit, um Filme basierend auf Benutzerpräferenzen und vergangenen Sehgewohnheiten zu empfehlen.
Bildverarbeitung
Gesichtserkennungssysteme, medizinische Bildgebungsanwendungen und selbstfahrende Fahrzeuge verlassen sich auf Kosinus-Ähnlichkeitswerte, um die Ähnlichkeit zwischen Bildern zu beurteilen. Sie verwenden konvolutionale neuronale Netzwerke, um Einbettungen für Bilder zu erzeugen und visuelle Muster unter ihnen zu erfassen.
Tipps zur Verwendung der Kosinus-Ähnlichkeit:
- Daten vorverarbeiten: Erwägen Sie, häufige Stoppwörter mit wenig bis keinem semantischen Wert zu entfernen – verwenden Sie auch Stemming oder Lemmatisierung, um Wörter auf ihre Grundform zu reduzieren und den Datensatz zu standardisieren.
- Termgewichtung verwenden: Verwenden Sie die TF-IDF-Technik, um seltenen Wörtern, die häufig in Dokumenten vorkommen, Gewichte zuzuweisen. Diese Gewichtung hilft bei der effizienten Vektordifferenzierung.
- Größere Datensatzgröße wählen: Die Verwendung größerer Datensätze ermöglicht es Ihnen, ein breiteres Spektrum an Themen und Stilen zu erkunden, was es einfacher macht, Ähnlichkeiten zu vergleichen.
Winkeln Sie Ihr Daten-Spiel an
Der Fokus der Kosinus-Ähnlichkeit auf Winkel anstelle von Magnitude macht sie ideal für Inhalts-Empfehlungen, Textanalysen, Dokumenten-Clusterbildung und Daten-Mining. Sie ist zweifellos die beste Wahl für den Vergleich von Transformator-Einbettungen aufgrund ihrer skaleninvarianten Natur und ihrer Fähigkeit, hochdimensionale Daten zu handhaben. Berücksichtigen Sie das Problem und die Datenanforderungen, um die am besten geeignete Methode zur Ähnlichkeitsberechnung zu finden.
Suchen Sie nach Software mit ereignisgesteuerter Architektur für die Echtzeit-Datenverarbeitung? Schauen Sie sich die besten Echtzeit-Analytik-Datenbanklösungen an.

Sagar Joshi
Sagar Joshi is a former content marketing specialist at G2 in India. He is an engineer with a keen interest in data analytics and cybersecurity. He writes about topics related to them. You can find him reading books, learning a new language, or playing pool in his free time.
