Abbiamo tutti sentito dire "la correlazione non implica causalità", ma cosa significa veramente?
Tutto si riduce a correlazione vs. regressione, misure di analisi statistica utilizzate per trovare connessioni tra due variabili, misurare le connessioni e fare previsioni. Il software di analisi statistica consente alle aziende di condurre questi processi complessi attraverso l'importazione, la preparazione e la modellazione statistica dei dati.
Indagare la relazione tra due variabili richiede di conoscere le differenze e le somiglianze tra correlazione e regressione. È comune confondersi tra questi due termini, poiché la correlazione può spesso portare alla regressione. Tuttavia, c'è una differenza chiave.
Qual è la differenza tra correlazione e regressione?
La differenza chiave tra correlazione e regressione è che la correlazione misura il grado di relazione tra due variabili indipendenti (x e y). Al contrario, la regressione riguarda come una variabile influisce su un'altra.
Essenzialmente, devi sapere quando usare la correlazione rispetto alla regressione. Usa la correlazione per riassumere la forza e il grado della relazione tra due o più variabili numeriche. Usa la regressione quando vuoi prevedere, ottimizzare o spiegare una risposta numerica tra le variabili (come x influenza y).
Correlazione vs. regressione: Panoramica
Misurare la correlazione e la regressione è comune per le aziende, ma è anche visibile nella nostra vita quotidiana. Ad esempio, hai mai visto qualcuno guidare un'auto costosa e pensato automaticamente che il conducente debba essere finanziariamente di successo? Oppure hai mai pensato che più corri durante il tuo allenamento mattutino, più peso perderai?
Entrambi sono esempi di correlazione e regressione nella vita reale, poiché vedi una variabile (un'auto di lusso o un lungo allenamento) e poi verifichi se c'è una relazione diretta con un'altra variabile (essere ricchi o perdere peso).
| Correlazione | Regressione | |
| Quando usare | Quando si riassume la relazione diretta tra due variabili | Per prevedere o spiegare la risposta numerica |
| Capace di quantificare la direzione della relazione? | Sì | Sì |
| Capace di quantificare la forza della relazione? | Sì | Sì |
| Capace di mostrare causa ed effetto? | No | Sì |
| Capace di prevedere e ottimizzare? | No | Sì |
| X e Y sono intercambiabili? | Sì | No |
| Usa un'equazione matematica? | No | y = a + b (x) |
Indipendentemente da ciò che stai usando per vedere correlazione e regressione, utilizzare una piattaforma di business intelligence è il modo migliore per analizzare i dati che stai osservando in modo da individuare facilmente quali intuizioni azionabili prendere. L'estrazione dei dati con il software di business intelligence consente un esame semplice di big data, dati in tempo reale e dati non strutturati e determina aree di miglioramento e altre tendenze notevoli.
Se non stai cercando piattaforme di business intelligence o piattaforme di analisi ma speri ancora di calcolare correlazione e regressione, puoi trovare entrambi utilizzando varie formule di Excel. Ricorda che una piattaforma BI è la tua migliore scommessa per aumentare l'efficienza e l'accuratezza.
Vuoi saperne di più su Software di analisi statistica? Esplora i prodotti Analisi Statistica.
Cos'è la correlazione?
Per definire semplicemente la correlazione, pensala come la combinazione delle parole "co" che significa insieme, e "relazione" che significa una connessione tra due quantità.
In questo senso, la correlazione è quando un cambiamento segue un cambiamento di una variabile in un'altra, sia diretto che indiretto. Le variabili si ritengono "non correlate" quando un cambiamento in una non influisce sull'altra. In breve, misura la relazione tra due variabili.
Cos'è la correlazione lineare?
A seconda della forma di una correlazione, potrebbe essere uno dei tre tipi.
- Correlazione lineare: Quando due variabili cambiano a un tasso costante, cioè il loro grafico di relazione deve essere una linea retta.
- Correlazione non lineare: Quando due variabili non cambiano a un tasso costante. Il grafico della relazione sarà una curva (parabole o iperbole.)
- Correlazione monotona: Quando due variabili si muovono nella stessa direzione relativa ma non a un tasso costante.
Ad esempio, supponiamo che le nostre due variabili siano x e y. Il tipo di correlazione tra queste due variabili può essere considerato positivo o negativo. Un cambiamento positivo sarebbe quando due variabili si muovono nella stessa direzione, il che significa che un aumento in una variabile causerà un aumento in un'altra. Quindi, se un aumento in x aumenta y, è positivamente correlato.
Un esempio di ciò sarebbe la domanda e il prezzo. Un aumento della domanda causa un aumento del prezzo. Il prezzo aumenta perché ci sono più consumatori che lo vogliono e sono disposti a pagare di più per esso.
Supponiamo che due variabili si muovano in direzioni opposte, come quando un aumento in una variabile risulta in una diminuzione in un'altra. Questo è noto come correlazione negativa. Un esempio di correlazione negativa è il prezzo e la domanda di due prodotti perché un aumento del prezzo (x) risulta in una diminuzione della domanda (y).
Conoscere come due variabili sono correlate consente di prevedere tendenze future, poiché sarai in grado di comprendere la relazione tra le variabili — o se non c'è alcuna relazione.
Coefficiente di correlazione
La correlazione mostra come le variabili sono correlate. Il coefficiente di correlazione (da -1 a 1) quantifica quella relazione. Un valore di 1 indica una correlazione positiva perfetta (entrambe le variabili si muovono nella stessa direzione), 0 significa nessuna correlazione, e -1 indica una correlazione negativa perfetta (le variabili si muovono in direzioni opposte).
Analisi della correlazione
Lo scopo principale della correlazione, attraverso la lente dell'analisi della correlazione, è consentire agli sperimentatori di conoscere l'associazione o l'assenza di una relazione tra due variabili. Quando queste variabili sono correlate, sarai in grado di misurare la forza della loro associazione.
In generale, l'analisi della correlazione mira a trovare il valore numerico che mostra la relazione tra le due variabili e come si muovono insieme.
Un vantaggio chiave della correlazione è che è un riassunto più conciso e chiaro della relazione tra le due variabili rispetto a quanto troverai con la regressione.
Formula della correlazione
La formula per il coefficiente di correlazione di Pearson (r), la misura di correlazione più comunemente usata, è:
r = ∑(xi - x̄) (yi - ȳ) / √ [∑(xi - x̄)² * ∑(yi - ȳ)²]
dove,
- xi è il valore i-esimo della variabile x
- yi è il valore i-esimo della variabile y
- x̄ è la media della variabile x
- ȳ è la media della variabile y
Esempi di correlazione
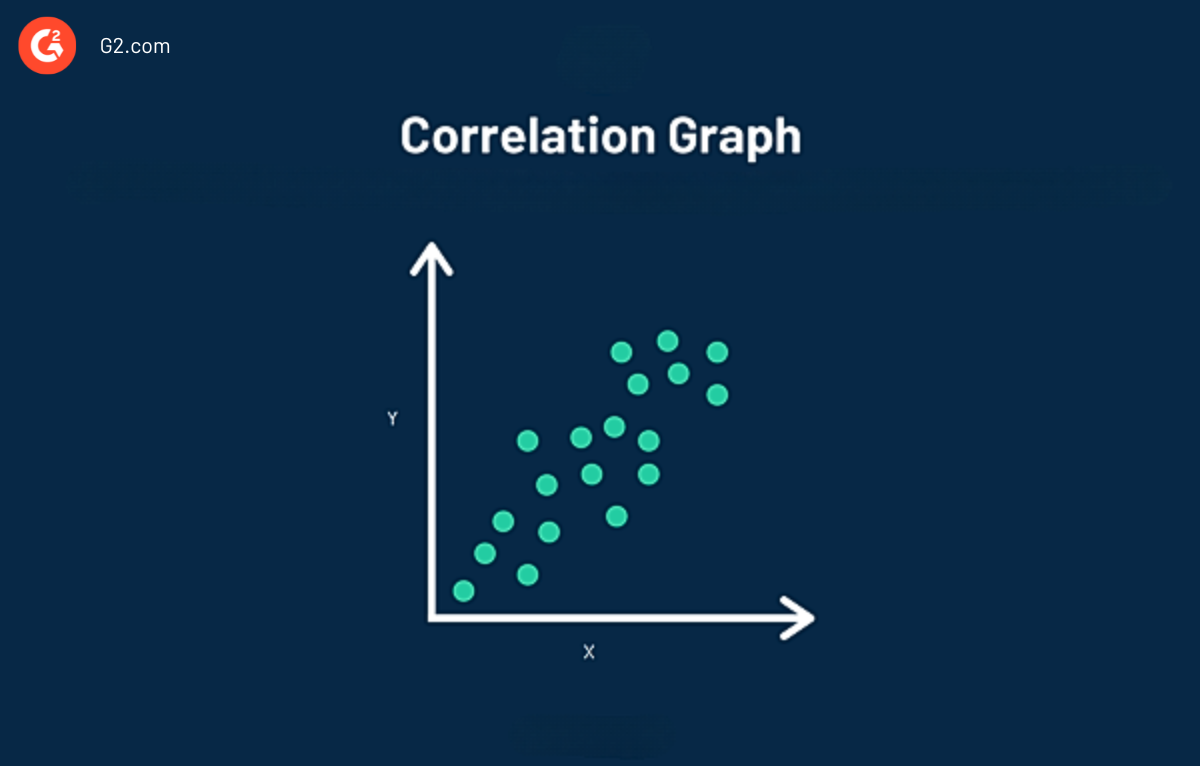
Un grafico di correlazione, noto anche come diagramma di dispersione, rende più facile vedere visivamente la correlazione tra due variabili. I dati in un grafico di correlazione sono rappresentati da un singolo punto. Nel grafico sopra, puoi osservare che la correlazione traccia vari punti di dati singoli.
Consideriamo la correlazione come scenari della vita reale. Oltre all'esempio di prezzo e domanda sopra, da un punto di vista finanziario, più a lungo investi, più interesse composto guadagnerai. Oppure, assumere più venditori risulta in un aumento delle entrate grazie all'azienda che effettua più vendite.
Ora guardiamo la correlazione da un punto di vista del marketing per vedere la forza di una relazione tra le due variabili. Ad esempio, potrebbe essere nel miglior interesse della tua azienda vedere se c'è una relazione prevedibile tra la vendita di un prodotto e fattori come il tempo, la pubblicità e il reddito dei consumatori.
Cos'è la regressione?
D'altra parte, la regressione riguarda come una variabile influisce su un'altra o cambiamenti in una variabile che innescano cambiamenti in un'altra, essenzialmente causa ed effetto. Implica che il risultato dipende da una o più variabili.
Ad esempio, mentre la correlazione può essere definita come la relazione tra due variabili, la regressione è come si influenzano a vicenda. Un esempio di ciò sarebbe come un aumento delle precipitazioni causerebbe la crescita di vari raccolti, proprio come una siccità causerebbe l'appassimento o la mancata crescita dei raccolti.
Quando la variabile dipendente aumenta mentre la variabile indipendente diminuisce, o viceversa, si chiama regressione negativa. Questo contrasta con una regressione positiva, dove sia le variabili dipendenti che indipendenti aumentano insieme.
Coefficiente di regressione
L'analisi della regressione modella la relazione tra una variabile dipendente (il risultato) e una o più variabili indipendenti (predittori). Il coefficiente di regressione, o pendenza, quantifica quanto la variabile dipendente cambia per ogni unità di cambiamento in una variabile indipendente.
Analisi della regressione
L'analisi della regressione aiuta a determinare la relazione funzionale tra due variabili (x e y) in modo da poter stimare la variabile sconosciuta e fare proiezioni future su eventi e obiettivi.
L'obiettivo principale dell'analisi della regressione è stimare i valori di una variabile casuale (z) basati sui valori delle tue variabili conosciute (o fisse) (x e y). L'analisi della regressione lineare è considerata la linea di miglior adattamento attraverso i punti dati.
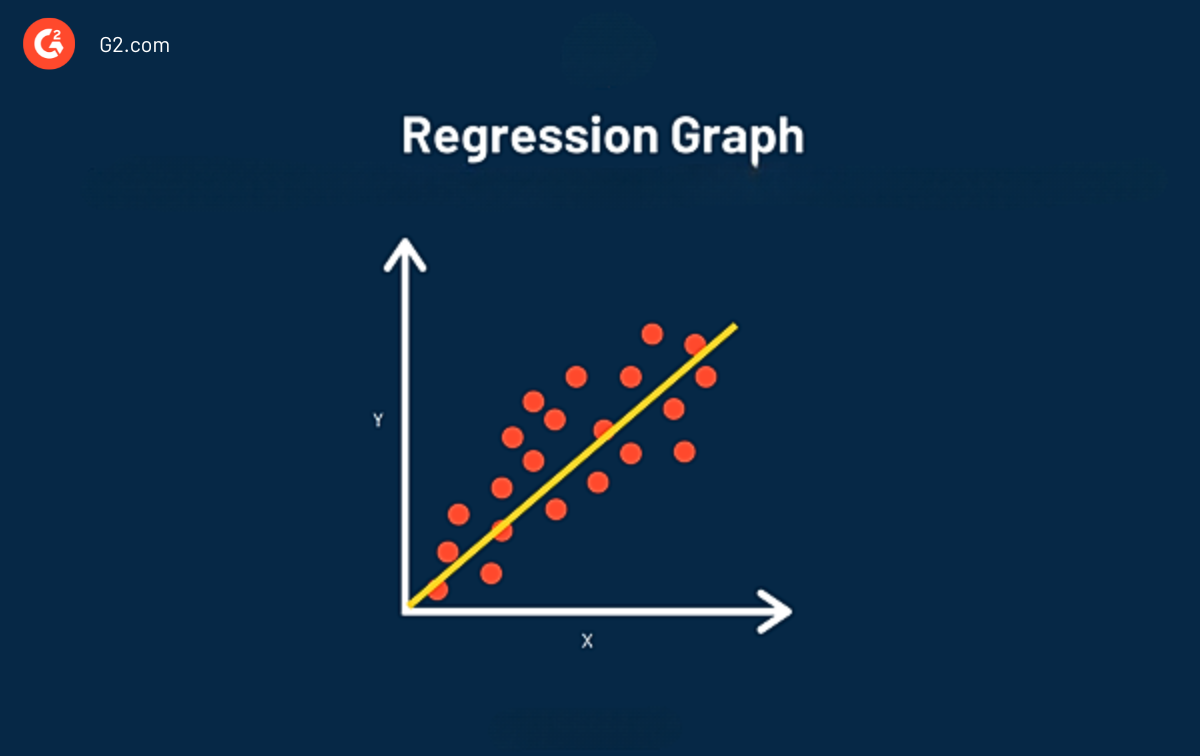
Il vantaggio principale dell'utilizzo della regressione all'interno della tua analisi è che fornisce uno sguardo dettagliato ai tuoi dati (più dettagliato della sola correlazione) e include un'equazione che può essere utilizzata per prevedere e ottimizzare i tuoi dati in futuro.
Quando la linea è tracciata usando la regressione, possiamo vedere due informazioni:
Formula della regressione
a → si riferisce all'intercetta y, il valore di y quando x = 0
b → si riferisce alla pendenza, o salita su corsa
La formula di previsione utilizzata per vedere come potrebbero apparire i dati in futuro è:
y = a + b (x)
Esempi di regressione
Quando si tratta di utilizzare la regressione, noi di G2 utilizziamo la regressione per prevedere certe tendenze, come come ci si aspetta che il nostro traffico cresca nei prossimi mesi.
Una persona che utilizza la regressione è un SEO e Data Analyst. Visualizzare i dati, analizzarli, identificare tendenze e prevedere come potrebbero apparire i dati in futuro è una grande parte del loro lavoro. Molti team si affidano al loro lavoro per stabilire obiettivi di team e comprendere come potrebbe apparire il nostro traffico in futuro.
Usano anche le previsioni dai modelli basati sulla regressione per stabilire obiettivi per metriche aziendali importanti, come l'acquisizione di parole chiave. Poiché le previsioni si basano su dati storici, questo dà all'azienda intuizioni su come sta attualmente andando rispetto alle tendenze di crescita passate.
Differenza tra correlazione e regressione
Ci sono alcune differenze chiave tra correlazione e regressione che sono importanti per comprendere i due.
- Fattori intercambiabili: La regressione stabilisce come x causa il cambiamento di y, e i risultati cambieranno se x e y vengono scambiati. Con la correlazione, x e y sono variabili che possono essere scambiate e ottenere lo stesso risultato.
- Punto dati singolo vs. equazione: La correlazione è una singola statistica, o punto dati, mentre la regressione è l'intera equazione con tutti i punti dati che sono rappresentati con una linea.
- Relazione vs. effetto: La correlazione mostra la relazione tra le due variabili, mentre la regressione ci permette di vedere come una influisce sull'altra.
- Causa ed effetto: I dati mostrati con la regressione stabiliscono una causa ed effetto. Quando uno cambia, cambia anche l'altro, e non sempre nella stessa direzione. Con la correlazione, le variabili si muovono insieme.
Ora è il momento di ricevere notizie e intrattenimento SaaS-y con la nostra newsletter di 5 minuti, G2 Tea, con leader ispiratori, opinioni audaci e previsioni coraggiose. Iscriviti qui sotto!
Somiglianze tra correlazione e regressione
Oltre alle differenze, ci sono alcune somiglianze chiave tra correlazione e regressione che possono aiutarti a comprendere meglio i tuoi dati.
- Entrambi lavorano per quantificare la direzione e la forza della relazione tra due variabili numeriche.
- Ogni volta che la correlazione è negativa, anche la pendenza della regressione (linea all'interno del grafico) sarà negativa.
- Ogni volta che la correlazione è positiva, anche la pendenza della regressione (linea all'interno del grafico) sarà positiva.
Domande frequenti su correlazione e regressione
D. Cosa sono la regressione e la correlazione in statistica?
La correlazione e la regressione sono tecniche utilizzate per analizzare la relazione tra due variabili quantitative. Mentre la correlazione misura la forza di una relazione lineare tra due variabili, la regressione in statistica misura come quelle variabili si influenzano a vicenda usando un'equazione.
D. Qual è una differenza chiave tra regressione e correlazione?
La correlazione determina la connessione o la relazione tra due variabili numeriche. La regressione si concentra su come quella relazione influenzerà ciascuna delle variabili nel tempo.
D. Dovrei usare la correlazione o la regressione?
Usa la correlazione per conoscere il grado di una relazione tra due variabili. Ma se vuoi analizzare l'effetto di come una variabile indipendente è numericamente associata alla variabile dipendente, usa la regressione.
D. Puoi fare correlazione e regressione insieme?
Sì, l'analisi della correlazione e della regressione può essere condotta insieme per misurare un set di dati e comprendere la relazione tra le variabili.
È più di causa ed effetto.
Anche se vengono studiati insieme, è chiaro che ci sono differenze e somiglianze evidenti tra correlazione e regressione.
Quando stai cercando di costruire un modello, un'equazione o prevedere una risposta chiave, usa la regressione. Se stai cercando di riassumere rapidamente la direzione e la forza di una relazione, la correlazione è la tua migliore scommessa.
Per concettualizzare ulteriormente i tuoi dati, usa software di visualizzazione dei dati e traccia le metriche aziendali e i KPI in tempo reale.
Questo articolo è stato originariamente pubblicato nel 2020. È stato aggiornato con nuove informazioni.

Mara Calvello
Mara Calvello is a Content and Communications Manager at G2. She received her Bachelor of Arts degree from Elmhurst College (now Elmhurst University). Mara writes content highlighting G2 newsroom events and customer marketing case studies, while also focusing on social media and communications for G2. She previously wrote content to support our G2 Tea newsletter, as well as categories on artificial intelligence, natural language understanding (NLU), AI code generation, synthetic data, and more. In her spare time, she's out exploring with her rescue dog Zeke or enjoying a good book.

