Imaginez ceci : vous faites des achats en ligne pour un ordinateur portable haute performance.
Vous cliquez sur un, et plusieurs suggestions similaires apparaissent. Elles sont proches de ce que vous recherchez mais ne sont pas identiques. Comment le site sait-il lesquelles sont pertinentes pour votre recherche ?
C'est là que la similarité cosinus entre en jeu – un outil mathématique qui mesure la similarité entre deux vecteurs non nuls dans un espace de haute dimension.
Les bases de données vectorielles dans les moteurs de recherche et les systèmes de recommandation utilisent la similarité cosinus pour comprendre à quel point les produits ou les requêtes de recherche dans une base de données correspondent en fonction de leurs représentations vectorielles. Comprendre ces relations et ces modèles parmi les éléments permet aux solutions de bases de données vectorielles de récupérer des suggestions personnalisées et précises qui vous incitent à naviguer – et peut-être même à acheter.
Qu'est-ce que la similarité cosinus ?
La similarité cosinus est une métrique mathématique qui mesure la similarité entre deux vecteurs dans un espace de produit intérieur ou multidimensionnel. Elle utilise le cosinus de l'angle entre deux vecteurs pour déterminer s'ils pointent dans la même direction, indépendamment de leurs magnitudes.
En d'autres termes, la similarité cosinus est le produit scalaire de deux vecteurs divisé par le produit de leurs magnitudes. Elle est également connue sous le nom de similarité d'Orchini et de coefficient de congruence de Tucker.
Les data scientists, les ingénieurs en apprentissage automatique et les développeurs de logiciels utilisent la similarité cosinus pour comparer des milliers de points de données et comprendre leurs relations sans se perdre dans les détails. Elle est largement utilisée pour mesurer la similarité dans les applications de fouille de texte, de récupération d'informations et d'analyse de texte.
D'autres mesures de similarité populaires incluent la distance euclidienne, la distance de Manhattan, la similarité de Jaccard et la distance de Minkowski.
Pourquoi la similarité cosinus est-elle importante ?
La similarité cosinus fournit un moyen robuste d'évaluer la similarité sémantique parmi des documents, ensembles de données et images de haute dimension et épars. Elle est efficace car elle se concentre sur l'orientation de deux vecteurs dans un espace, mesurant leur similarité indépendamment de leur magnitude.
Les applications d'analyse de texte utilisant la fréquence des termes-inverse de la fréquence des documents (TF-IDF), Word2Vec et les représentations d'encodeurs bidirectionnels de transformateurs (BERT) dérivent des vecteurs de mots avec de grandes dimensions mais peu de chevauchement. Les métriques de similarité traditionnelles comme la distance euclidienne sont sensibles aux longueurs de vecteurs et ne peuvent pas gérer ces vecteurs. La similarité cosinus peut facilement se concentrer sur la corrélation des données dans de tels scénarios.
La similarité cosinus aide également les applications de récupération d'informations à classer les documents en fonction de leur correspondance avec une requête, même lorsque les documents varient en longueur ou en complexité.
La scalabilité de la similarité cosinus dans l'espace vectoriel de haute dimension la rend inestimable pour les bases de données vectorielles, où trouver rapidement et précisément les voisins les plus proches est nécessaire pour la récupération d'images, les systèmes de recommandation et la détection d'anomalies.
Le traitement du langage naturel (NLP) repose sur la similarité cosinus pour comparer efficacement les embeddings vectoriels. Cette comparaison d'embeddings aide les algorithmes de NLP à classer, regrouper ou recommander du contenu en fonction de la similarité sémantique des documents.
Vous voulez en savoir plus sur Logiciel de base de données vectorielle ? Découvrez les produits Base de données vectorielle.
Comment fonctionne la similarité cosinus ?
La similarité cosinus quantifie la similarité entre deux vecteurs en calculant le cosinus de l'angle entre eux. Voici le détail de la façon dont la similarité cosinus fonctionne dans des environnements de données éparses et de haute dimension.
- Représentation vectorielle : La première étape consiste à convertir des objets comme des mots, des documents, des images ou des textes en vecteurs dans un espace de haute dimension. Chaque dimension vectorielle représente un seul objet, avec sa valeur montrant la fréquence vectorielle ou son importance.
- Produit scalaire : Le produit scalaire quantifie la relation entre deux vecteurs en multipliant leurs composants correspondants et en additionnant les résultats. Calculer ce produit scalaire est vital pour comprendre l'alignement entre les vecteurs dans la même direction.
- Calcul de la magnitude : L'étape suivante consiste à calculer les longueurs ou magnitudes de chaque vecteur.
- Similarité cosinus : Le score de similarité cosinus est le produit scalaire divisé par le produit des magnitudes des deux vecteurs.
Diviser le produit scalaire par le produit des magnitudes des vecteurs normalise le résultat de similarité à une plage entre -1 et 1. Cette normalisation garantit que le score de similarité reflète uniquement l'angle d'orientation des vecteurs, pas leur magnitude. Elle mesure de manière cohérente la similarité des vecteurs, indépendamment de l'échelle des données.
Comment calculer la similarité cosinus
Calculer la similarité cosinus nécessite de trouver le produit scalaire de deux vecteurs. Ensuite, multipliez les magnitudes de ces deux vecteurs. Maintenant, divisez le produit scalaire par le produit des magnitudes pour trouver le score de similarité cosinus.
Formule de similarité cosinus
Le score de similarité cosinus entre deux vecteurs, A et B, est calculé en utilisant la formule ci-dessous :
Similarité Cosinus (A, B) = (A·B) / (||A|| * ||B||)
Où,
A · B est le produit scalaire des vecteurs A et B
||A|| et ||B|| représentent la longueur ou magnitude des deux vecteurs A et B
||A|| * ||B|| dénote le produit des magnitudes des vecteurs A et B
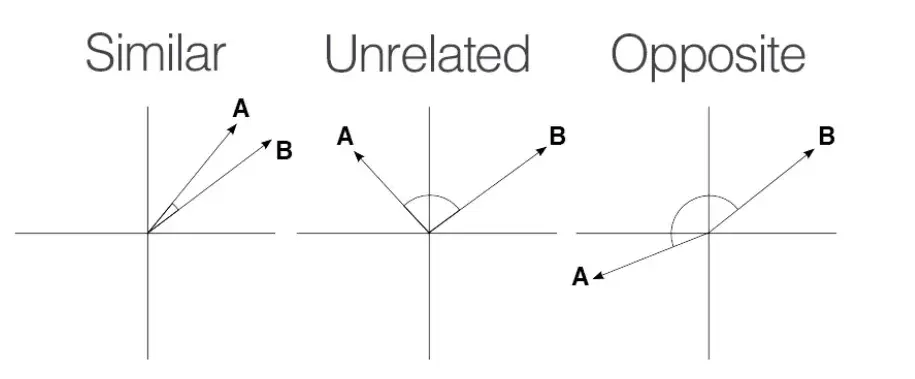
La similarité cosinus varie entre -1 et 1.
 Source: Medium
Source: Medium
Un score de 1 signifie que les vecteurs sont parfaitement alignés ou proportionnels, indiquant une similarité maximale.
Un score de 0 implique que les vecteurs sont orthogonaux, ce qui signifie qu'ils n'ont aucune similarité.
Un score de -1 montre que les vecteurs sont parfaitement opposés, ce qui signifie qu'ils pointent dans des directions opposées mais ont la même magnitude.
Exemple de similarité cosinus
Calculons la similarité cosinus entre les vecteurs A et B.
Le vecteur A a des valeurs, A = { 1, 9, 3, 6 } Le vecteur ‘B’ a des valeurs, B = { 1, 7, 0, 1 }
Produit scalaire : A·B = 1×1 + 9×7 + 3×0 + 6×1 =70
Magnitude de A : ||A|| = √(1² + 9² + 3² + 6²) = √(1 + 81 + 9 + 36) = √127 ≈ 11.27
Magnitude de B : ||B|| = √(1² + 7² + 0² + 1²) = √(1 + 49 + 0 + 1) = √51 ≈ 7.14
Similarité Cosinus = (A · B) / (||A|| * ||B||) = 70 / (11.27 × 7.14) ≈ 0.87
La similarité cosinus entre les vecteurs A et B est d'environ 0.87, ce qui montre une similarité substantielle entre eux.
Bibliothèques pour le calcul de la similarité cosinus
Calculer la similarité cosinus est simple mais peut être difficile lorsque l'on travaille avec de grands ensembles de données. Dans de telles situations, vous pouvez utiliser des langages de programmation comme Python et des bibliothèques et outils comme Matlab, SciKit-Learn, TensorFlow et SciPy.
NumPy
NumPy est une puissante bibliothèque Python pour les calculs numériques. Elle prend en charge les opérations sur les tableaux multidimensionnels, les matrices et les fonctions mathématiques, ce qui la rend idéale pour les calculs de similarité cosinus.
Comment calculer la similarité cosinus en utilisant NumPy
# importer les bibliothèques requises
import numpy as np
from numpy.linalg import norm
# définir deux listes ou tableaux
A = np.array([1, 9, 3, 6])
B = np.array([1, 7, 0, 1])
print("A:", A)
print("B:", B)
# calculer la similarité cosinus
cosine = np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B))
print("Similarité Cosinus:", cosine)
SciKit-Learn
SciKit-Learn est une bibliothèque d'apprentissage automatique basée sur Python avec des fonctions intégrées pour les tâches d'analyse de données, y compris la similarité cosinus. Le module sklearn.metrics.pairwise offre une fonction cosine_similarity pour gérer à la fois les matrices denses et éparses.
Comment calculer la similarité cosinus en utilisant SciKit-Learn
# importer les bibliothèques requises
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
# définir les vecteurs
A = np.array([[1, 9, 3, 6]])
B = np.array([[1, 7, 0, 1]])
# calculer la similarité cosinus
cosine_sim = cosine_similarity(A, B)
print("Similarité Cosinus:", cosine_sim[0][0])
SciPy
SciPy est une autre bibliothèque populaire basée sur Python pour le calcul scientifique. Construite sur NumPy, SciPy propose des fonctions optimisées qui calculent la similarité cosinus pour de grands ensembles de données. Son module scipy.spatial.distance inclut une fonction de calcul de distance cosinus, que vous pouvez utiliser pour calculer la similarité cosinus.
Comment calculer la similarité cosinus en utilisant SciPy
# importer les bibliothèques requises
import numpy as np
from scipy.spatial.distance import cosine
# définir les vecteurs
A = np.array([1, 9, 3, 6])
B = np.array([1, 7, 0, 1])
# calculer la distance cosinus
cosine_distance = cosine(A, B)
# calculer la similarité cosinus
cosine_similarity = 1 - cosine_distance
print("Similarité Cosinus:", cosine_similarity)
Gensim
Gensim est une bibliothèque Python largement utilisée pour la modélisation de sujets et le traitement du langage naturel. Elle propose des fonctions intégrées pour calculer la similarité cosinus entre un grand volume de documents textuels et de vecteurs de mots.
Comment calculer la similarité cosinus en utilisant Gensim
# importer les bibliothèques requises
from gensim import corpora
from gensim.matutils import sparse2full
from gensim.similarities import MatrixSimilarity
from gensim.models import TfidfModel
import numpy as np
# documents d'exemple
documents = [
"J'aime jouer au football.",
"Le football est un grand sport.",
"J'aime regarder des films.",
"Les films sont divertissants.",
]
# tokeniser et prétraiter
texts = [[word.lower() for word in doc.split()] for doc in documents]
# créer un dictionnaire et un corpus
dictionary = corpora.Dictionary(texts)
corpus = [dictionary.doc2bow(text) for text in texts]
# créer un modèle TF-IDF
tfidf_model = TfidfModel(corpus)
tfidf_corpus = tfidf_model[corpus]
# créer un index de similarité
index = MatrixSimilarity(tfidf_corpus)
# calculer la similarité du premier document avec tous les autres
similarities = index[tfidf_corpus[0]]
# imprimer les similarités
print("Similarités Cosinus pour le Document 0:", similarities)
TensorFlow et PyTorch
TensorFlow et PyTorch sont des bibliothèques populaires d'apprentissage profond qui aident à mesurer la similarité entre des vecteurs de caractéristiques de haute dimension.
Comment calculer la similarité cosinus en utilisant TensorFlow
# importer les bibliothèques requises
import tensorflow as tf
# définir les vecteurs
A = tf.constant([1.0, 9.0, 3.0, 6.0])
B = tf.constant([1.0, 7.0, 0.0, 1.0])
# calculer la similarité cosinus
def cosine_similarity(A, B):
# calculer le produit scalaire
dot_product = tf.reduce_sum(A * B)
# calculer la norme (magnitude) des vecteurs
norm_A = tf.sqrt(tf.reduce_sum(tf.square(A)))
norm_B = tf.sqrt(tf.reduce_sum(tf.square(B)))
# calculer la similarité cosinus
cosine_sim = dot_product / (norm_A * norm_B)
return cosine_sim
similarity = cosine_similarity(A, B)
print("Similarité Cosinus:", similarity.numpy())
# calculer la similarité cosinus
cosine_similarity = 1 - cosine_distance
print("Similarité Cosinus:", cosine_similarity)
Lors de l'utilisation de PyTorch, les développeurs peuvent utiliser torch.tensor() pour créer des objets tensoriels et utiliser la fonction torch.norm() pour calculer la norme euclidienne des vecteurs.
Envisagez d'utiliser les conseils ci-dessous pour optimiser les calculs cosinus en Python :
- Optez pour des bibliothèques optimisées. Utilisez les opérations vectorisées de NumPy ou SciKit-Learn pour calculer la similarité cosinus et réduire la surcharge des boucles Python. Ces bibliothèques sont également plus rapides que le Python de base.
- Utilisez Numba. Numba est un compilateur juste-à-temps (JIT) open-source pour le code Python et NumPy. Il vous aide à paralléliser automatiquement les calculs de similarité cosinus en utilisant plusieurs unités centrales de traitement (CPU).
- Employez des matrices éparses. Envisagez d'utiliser les représentations de matrices éparses de SciPy lorsque vous traitez des ensembles de données avec de nombreuses valeurs nulles. Cela vous aidera à économiser de la mémoire et du temps de calcul pour les tâches d'analyse de similarité de texte et de document.
- Utilisez Cython pour la compilation de code. Cython permet aux développeurs d'écrire des codes de type C avec une syntaxe de type Python. L'utiliser pour la compilation de code les aide à atteindre des vitesses similaires à celles du C ou du C++ tout en conservant la facilité de la syntaxe Python.
- Utilisez les algorithmes ANN. Les algorithmes de voisins les plus proches approximatifs ou ANN comme KD-Tress ou le hachage sensible à la localité (LSH) aident à trouver des vecteurs similaires sans calculer la similarité cosinus. Ces algorithmes peuvent être bénéfiques pour les applications à grande échelle.
- Accédez aux GPU. Utiliser des unités de traitement graphique ou GPU avec des bibliothèques Python comme TensorFlow peut également aider à atteindre un débit plus élevé lors du travail avec de grands ensembles de données de haute dimension.
Similarité cosinus vs. autres méthodes de calcul de similarité
La similarité cosinus n'est pas la seule méthode pour mesurer la similarité entre des objets dans un ensemble de données. D'autres méthodes de calcul de similarité populaires sont :
Distance euclidienne
La distance euclidienne mesure la distance en ligne droite entre deux points dans l'espace euclidien. Elle est toujours soit nulle, soit positive. Vous ne pourrez peut-être pas trouver une distance euclidienne significative dans des espaces de haute dimension car les points ont tendance à converger.
La similarité cosinus est idéale pour les données de haute dimension ou l'analyse de texte où la magnitude du vecteur n'est pas essentielle. La similarité euclidienne fonctionne mieux pour les espaces de basse dimension où la magnitude du vecteur est vitale.
Distance de Manhattan
Cela mesure la distance entre deux points dans un chemin en grille en additionnant les différences absolues entre leurs coordonnées. Contrairement à la distance euclidienne, la distance de Manhattan est moins sensible aux valeurs aberrantes, c'est pourquoi elle est adaptée aux tâches de regroupement.
Utilisez la distance de Manhattan pour considérer les différences absolues entre les coordonnées mais la similarité cosinus lorsque la direction des vecteurs est plus importante que la magnitude.
Distance de Hamming
La distance de Hamming compare deux chaînes de données binaires de longueur égale en quantifiant le nombre de positions de bits entre deux bits. Elle mesure le nombre de positions où les symboles correspondants de deux chaînes diffèrent.
La distance de Hamming est toujours un entier non négatif puisque la distance est le total des décalages. Les tâches de classification en apprentissage automatique et les algorithmes de détection d'erreurs utilisent la distance de Hamming pour comparer les vecteurs binaires.
Similarité de Jaccard
La similarité de Jaccard, également connue sous le nom de coefficient de Jaccard ou indice de Jaccard, est une autre mesure de proximité qui calcule la similarité entre deux vecteurs ou objets binaires asymétriques. Vous pouvez la calculer en divisant la taille de l'intersection des ensembles par la taille de l'union des ensembles.
La similarité de Jaccard est idéale pour comparer la présence ou l'absence de termes, tandis que la similarité cosinus excelle à mesurer l'angle entre les vecteurs dans des données denses avec des termes qui se chevauchent.
Avantages de la similarité cosinus
L'avantage principal est que la similarité cosinus capture l'aspect directionnel des données sans être affectée par les changements de magnitude des vecteurs. Les applications d'analyse de texte, les systèmes de recommandation et les solutions NLP utilisent la similarité cosinus pour faciliter le calcul et réduire efficacement les dimensions des vecteurs.
- Invariance de magnitude : La similarité cosinus mesure la direction de deux vecteurs et ne fausse pas le score de proximité même lorsqu'ils diffèrent en longueur. Sa nature invariante à l'échelle la rend idéale pour les moteurs de recherche et les applications basées sur le texte, où elle se concentre sur la question de savoir si les vecteurs couvrent des sujets similaires au lieu de la longueur, du nombre de mots ou de la verbosité.
- Scalabilité pour les données éparses : La similarité cosinus utilise la pertinence directionnelle pour compresser efficacement les données avec de grandes dimensions. Le résultat est un temps de calcul rapide pour les ensembles de données épars et de haute dimension, ce qui rend la similarité cosinus idéale pour les bases de données vectorielles et les systèmes de récupération d'images.
- Réduction de la dimensionnalité : La similarité cosinus est compatible avec des techniques comme l'analyse en composantes principales (PCA) et l'embedding de voisin stochastique distribué (t-SNE). Ces méthodes réduisent le nombre de dimensions tout en préservant la variance dans un ensemble de données. L'attention de la similarité cosinus aux relations angulaires garantit que les points de données restent robustes même après ces transformations qui mappent les vecteurs dans un espace de dimension inférieure.
- Similarité sémantique : Le score de similarité cosinus utilise des modèles d'espace vectoriel pour comparer les mots en fonction de leurs significations au lieu des comptes de mots bruts ou des similarités syntaxiques. Les meilleurs moteurs de recherche de bases de données vectorielles s'appuient sur cette capacité pour mesurer la distance entre les mots ou phrases vectorisés dans les tâches d'analyse de sentiment, de modélisation de sujets et de traduction automatique.
Inconvénients de la similarité cosinus
Malgré ses nombreux avantages, la similarité cosinus souffre d'inconvénients, notamment :
- Malédiction de la dimensionnalité : La similarité cosinus peut rencontrer des difficultés dans l'analyse des données dans des espaces de haute dimension, un phénomène connu sous le nom de malédiction de la dimensionnalité. Les distances accrues entre les points de données provoquent la convergence des angles entre les vecteurs, rendant difficile leur différenciation en utilisant la similarité cosinus.
- Sensibilité aux données éparses : La similarité cosinus a également du mal à fournir des informations significatives dans des ensembles de données épars avec de nombreuses entrées nulles dans les vecteurs.
- Ne considère pas la différence absolue : Comme la similarité cosinus se concentre sur un angle au lieu de la magnitude des vecteurs, elle peut négliger les différences de magnitude, qui peuvent transmettre des informations contextuelles cruciales.
- Dépendance élevée à la représentation vectorielle : La similarité cosinus peut renvoyer des résultats inexacts pour des représentations vectorielles mal construites de documents.
Applications de la similarité cosinus
La similarité cosinus est utilisée dans la récupération d'informations, la fouille de texte, les systèmes de recommandation, le traitement d'images, la classification de documents et le regroupement.
« Nous utilisons la similarité cosinus pour mesurer la similarité entre le texte original et le texte généré par l'IA. Cela nous aide à améliorer l'originalité du texte généré par l'IA et à le personnaliser pour la satisfaction et l'engagement des utilisateurs. »
Robert Brown
Co-fondateur de AI Humanize
Récupération d'informations
Les systèmes de récupération d'informations comme les moteurs de recherche utilisent la similarité cosinus pour trouver des documents pertinents dans la base de données pour les requêtes de recherche. Cette recherche de similarité garantit que les utilisateurs obtiennent des documents précieux. Dans ces cas, l'embedding de texte repose sur des modèles complexes de réseaux de neurones artificiels comme Word2Vec, GloVe ou des LLM comme GPT, BERT et LLaMa.
Systèmes de recommandation
Les plateformes de streaming de films comme Netflix s'appuient sur la similarité cosinus pour partager des recommandations basées sur l'historique de visionnage des utilisateurs. Ces systèmes considèrent chaque film et utilisateur comme des vecteurs. Après avoir généré des embeddings vectoriels en utilisant la factorisation de matrice ou les autoencodeurs, ils utilisent la similarité cosinus pour recommander des films en fonction des préférences des utilisateurs et des habitudes de visionnage passées.
Traitement d'images
Les systèmes de reconnaissance faciale, les applications d'imagerie médicale et les véhicules autonomes s'appuient sur les scores de similarité cosinus pour évaluer la similarité entre les images. Ils utilisent des réseaux de neurones convolutifs pour générer des embeddings pour les images et capturer les motifs visuels parmi elles.
Conseils pour utiliser la similarité cosinus :
- Prétraiter les données : Envisagez de supprimer les mots vides courants avec peu ou pas de valeur sémantique – utilisez également le stemming ou la lemmatisation pour réduire les mots à leur forme de base et standardiser l'ensemble de données.
- Utiliser la pondération des termes : Employez la technique TF-IDF pour attribuer des poids aux mots rares apparaissant fréquemment dans les documents. Cette pondération aide à une différenciation efficace des vecteurs.
- Optez pour une taille de jeu de données plus grande : Utiliser des ensembles de données plus grands vous permet d'explorer une gamme plus large de sujets et de styles, ce qui facilite la comparaison des similarités.
Améliorez votre jeu de données
Le focus de la similarité cosinus sur les angles au lieu de la magnitude la rend idéale pour la recommandation de contenu, l'analyse de texte, le regroupement de documents et la fouille de données. C'est sans aucun doute le meilleur choix pour comparer les embeddings de transformateurs en raison de sa nature invariante à l'échelle et de sa capacité à gérer des données de haute dimension. Envisagez le problème et les exigences des données pour trouver la méthode de calcul de similarité la plus appropriée.
Vous cherchez un logiciel avec une architecture événementielle pour le traitement de données en temps réel ? Découvrez les meilleures solutions de bases de données analytiques en temps réel.

Sagar Joshi
Sagar Joshi is a former content marketing specialist at G2 in India. He is an engineer with a keen interest in data analytics and cybersecurity. He writes about topics related to them. You can find him reading books, learning a new language, or playing pool in his free time.
